Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(M\left(x\right)+N\left(x\right)\)
\(=5x^3-x^2-4+2x^4-2x^2+2x+1\)
\(=2x^4+5x^3-3x^2+2x-3\)
\(M\left(x\right)-N\left(x\right)\)
\(=5x^3-x^2-4-\left(2x^4-2x^2+2x+1\right)\)
\(=5x^3-x^2-4-2x^4+2x^2-2x-1\)
\(=-2x^4+5x^3+x^2-2x-5\)
\(M\left(x\right)+P\left(x\right)=N\left(x\right)\)
\(\Rightarrow P\left(x\right)=N\left(x\right)-M\left(x\right)\)
\(\Rightarrow P\left(x\right)=2x^4-2x^2+2x+1-\left(5x^3-x^2-4\right)\)
\(\Rightarrow P\left(x\right)=2x^4-2x^2+2x+1-5x^3+x^2+4\)
\(\Rightarrow P\left(x\right)=2x^4-5x^3-x^2+2x+5\)

\(a,A\left(x\right)=2x+3\)
Có \(2x+3=0\)
\(\Rightarrow x=-\frac{3}{2}\)
Vậy \(-\frac{3}{2}\)là 1 nghiệm của đa thức A(x)
\(b,B\left(x\right)=4x^2-25\)
\(\Rightarrow B\left(x\right)=\left(2x\right)^2-25\)
Có \(B\left(x\right)=0\Rightarrow\left(2x\right)^2-25=0\)
\(\Rightarrow\left(2x\right)^2=25\)
\(\Rightarrow\orbr{\begin{cases}2x=5\\2x=-5\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{5}{2}\\x=-\frac{5}{2}\end{cases}}\)
Vậy -5/2 là 1 nghiệm của B(x)
\(c,C\left(x\right)=x^2-7\)
Có \(C\left(x\right)=0\Leftrightarrow x^2-7=0\)
\(\Rightarrow x^2=7\)
\(\Rightarrow x=\orbr{\begin{cases}\sqrt{7}\\-\sqrt{7}\end{cases}}\)
Vậy \(\sqrt{7};-\sqrt{7}\)là 2 nghiệm của C(x)
\(d,D\left(x\right)=x\left(1-2x\right)+\left(2x^2-x+4\right)\)
\(D\left(x\right)=x-2x^2+2x^2-x+4\)
\(D\left(x\right)=4\)
Vậy D(x) vô nghiệm
+) Ta có: A(x) = 2x + 3 = 0
(=) 2x = -3
(=) x = \(\frac{-3}{2}\).
+) Ta có: B(x) = 4x2 -25 = 0
(=) 4x2 = 25
(=) (2x)2 = 52
=> 2x = 5
(=) x = \(\frac{5}{2}\).

a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
Thu gọn: P(x) = 3x2 - 5 + x4 - 3x3 - x6 - 2x2 - x3
= x2 - 5 + x4 - 4x3 - x6
Sắp xếp: P(x) = -5 + x2 - 4x3 + x4 - x6
Thu gọn: Q(x) = x3 + 2x5 - x4 + x2 - 2x3 + x - 1= -x3 +2x5 - x4 + x2 + x - 1
Sắp xếp: Q(x) = -1 + x + x2 - x3 - x4 + 2x5
b) Ta có:
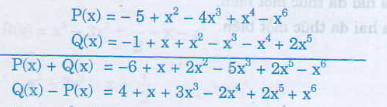 .
.
a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
Thu gọn: P(x) = 3x2 - 5 + x4 - 3x3 - x6 - 2x2 - x3
= x2 - 5 + x4 - 4x3 - x6
Sắp xếp: P(x) = -5 + x2 - 4x3 + x4 - x6
Thu gọn: Q(x) = x3 + 2x5 - x4 + x2 - 2x3 + x - 1= -x3 +2x5 - x4 + x2 + x - 1
Sắp xếp: Q(x) = -1 + x + x2 - x3 - x4 + 2x5
b) Ta có:
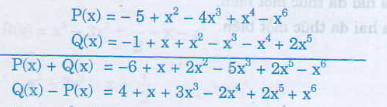

Ta có:
P(x) = 2x4 –x - 2x3 + 1
Q(x) = 5x2 – x3 + 4x
H(x) = -2x4 + x2 + 5.
Sắp xếp các đa thức theo lũy thừa giảm dần rồi xếp các số hạng đồng dạng theo cùng cột dọc ta được:
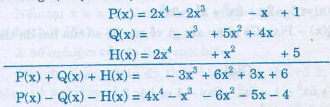
ta có:
P(x) = 2x4 –x – 2x3 + 1
Q(x) = 5x2 – x3 + 4x
H(x) = -2x4 + x2 + 5.
Sắp xếp các đa thức theo lũy thừa giảm dần rồi xếp các số hạng đồng dạng theo cùng cột dọc ta được:


Giải:
a) Để đa thức có nghiệm thì
\(x^2-4x=0\)
\(\Leftrightarrow\left(x-4\right)x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
Vậy ...
b) Để đa thức có nghiệm thì
\(\left(x-3\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-4\end{matrix}\right.\)
Vậy ...
c) Để đa thức có nghiệm thì
\(\left(x-1\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x^2+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x\in\varnothing\end{matrix}\right.\)
Vậy ...
Các ý còn lại làm tương tự.
a) \(\Leftrightarrow x\left(x-4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
...
..
f) \(\Leftrightarrow x^2+\dfrac{7}{2}x+\dfrac{5}{2}=0\)
\(\Leftrightarrow\left(x^2+\dfrac{7}{4}x\right)+\left(\dfrac{7}{4}x+\dfrac{7.7}{4.4}\right)+\dfrac{5}{2}-\dfrac{49}{16}=0\)
\(\Leftrightarrow x\left(x+\dfrac{7}{4}\right)+\dfrac{7}{4}\left(x+\dfrac{7}{4}\right)=\dfrac{49-5.8}{16}=\dfrac{9}{16}\)
\(\Leftrightarrow\left(x+\dfrac{7}{4}\right)^2=\left(\dfrac{3}{4}\right)^2\)
\(\left|x+\dfrac{7}{4}\right|=\dfrac{3}{4}\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{7}{4}-\dfrac{3}{4}=\dfrac{-5}{2}\\x=-\dfrac{7}{4}+\dfrac{3}{4}=-1\end{matrix}\right.\)

\(f\left(x\right)+h\left(x\right)-g\left(x\right)\)
\(=\left(5x^4+3x^2+x-1\right)+\left(-x^4+3x^3-2x^2-x+2\right)\)
\(-\left(2x^4-x^3+x^2+2x+1\right)\)
\(=\left(5x^4-x^4-2x^4\right)+\left(3x^3+x^3\right)+\left(3x^2-2x^2-x^2\right)\)
\(+\left(x-x-2x\right)+\left(-1+2-1\right)\)
\(=2x^4+4x^3-2x\)

Ta có : \(A\left(x\right)+C\left(x\right)=3-2x^3-x+x^2-4x^2-3x^2-2x^3+3x-2\)
\(=-4x^3-6x^2+2x+1\)
\(A\left(x\right)-B\left(x\right)=3-2x^3-x+x^2-4x^2-\left(-x^3+9x^2-8x-5-2x^2\right)\)
\(=3-2x^3-x+x^2-4x^2+x^3-9x^2+8x+5+2x^2\)
\(=-x^3-10x^2+7x+8\)
Đáp án A
A
nha bn
Học tốt