Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
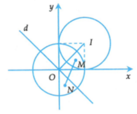

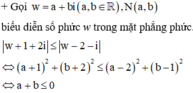
=> Tập hợp các điểm M là nửa mặt phẳng không chứa điểm I(1;1), có bờ là đường thẳng x + y = 0 (d)


Đặt z = a + bi với a , b ∈ R
Khi đó
z - 2 i z - 2 = a + b - 2 i a - 2 + b i = a + b - 2 i a - 2 - b i a - 2 2 + b 2 = a a - 2 + b b - 2 a - 2 2 + b 2 + a - 2 b - 2 - a b a - 2 2 + b 2
z - 2 i z - 2 là số ảo khi và chỉ khi
a a - 2 + b b - 2 a - 2 2 + b 2 = 0 ⇔ a 2 + b 2 = 2 a + b a - 2 2 + b 2 ≠ 0
Ta có
P = z - 1 + z - i = a - 1 + b i + a + b - 1 i = a - 1 2 + b + a 2 + b - 1 2 = a 2 + b 2 - 2 a + 1 + a 2 + b 2 - 2 b + 1 = 2 a + b - 2 a + 1 + 1 a + b - 2 a + 1 = 1 + 2 b + 1 + 2
Áp dụng bất đẳng thức Cauchy ta có: 2 a + b = a 2 + b 2 ≥ 1 2 a + b 2
Suy ra a + b ≤ 4
Do đó P 2 ≤ 2 2 + 2 a + b ≤ 20 ⇔ P ≤ 2 5
Dấu “=” xảy ra khi và chỉ khi a = b = 2
Vậy maxP = 2 5 đạt được khi z = 2 + 2i
Đáp án C



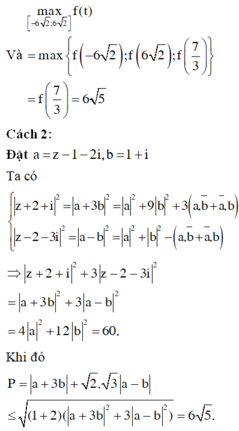
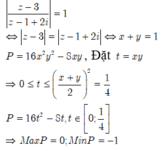



Đáp án D
Giả sử z = x + y i , x , y ∈ ℝ . Từ giả thiết ta có 2 x + y i − i = 2 + i x + y i
⇔ 2 x + 2 y − 1 i = 2 − y + x i ⇔ 4 x 2 + 2 y − 1 2 = y − 2 2 + x 2 ⇔ x 2 + y 2 = 1
Suy ra tập hợp các điểm A, B biểu diễn hai số phức z 1 , z 2 là đường tròn tâm O 0 ; 0 , bán kính R = 1 = O A = O B .
Giả sử z 1 = a 1 + b 1 i , z 2 = a 2 + b 2 i , a 1 , a 2 , b 1 , b 2 ∈ ℝ . Khi đó A a 1 ; b 1 , B a 2 ; b 2 .
Từ giả thiết z 1 − z 2 = 1 ta được:
a 1 − a 2 + b 1 − b 2 i = 1 ⇔ a 1 − a 2 2 + b 1 − b 2 2 = 1 ⇔ A B = 1
Từ đó O A = O B = A B ⇒ Δ O A B đều cạnh bằng 1.
Gọi M là trung điểm AB thì M a 1 + b 1 2 ; a 2 + b 2 2 và O M = A B 3 2 = 3 2 .
Khi đó
P = z 1 + z 2 = a 1 + a 2 + b 1 + b 2 i = a 1 + a 2 2 + b 1 + b 2 2
= 2 a 1 + a 2 2 2 + b 1 + b 2 2 2 = 2 O M = 2. 3 2 = 3