Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề sai bạn nhé. Đưa dữ kiện 3 ẩn bắt tính biểu thức chứa 2 ẩn làm sao làm được ?
Bạn kiểm tra lại nha

Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{y+x+t}=\dfrac{y}{z+t+x}=\dfrac{y}{t+x+y}=\dfrac{t}{x+y+z}=\dfrac{x+y+z+t}{3\left(x+y+z+t\right)}=\dfrac{1}{3}\)
\(\Rightarrow\left\{{}\begin{matrix}x+y+z=3t\\y+z+t=3x\\z+t+x=3y\\t+x+y=3z\end{matrix}\right.\)
\(\Rightarrow x=y=z=t\)
Thay vào P ta được :
\(P=1+1+1+1=4\)

Giải:
a) \(-1313x^2y.2xy^3\)
\(=\left(-1313.2\right)\left(x^2.x\right)\left(y.y^3\right)\)
\(=-2626x^3y^4\)
Bậc của đơn thức là: \(3+4=7\)
b) \(1414x^3y.\left(-2x^3y^5\right)\)
\(=\left[1414.\left(-2\right)\right]\left(x^3.x^3\right)\left(y.y^5\right)\)
\(=-2828x^6y^6\)
Bậc của đơn thức là: \(6+6=12\).
Chúc bạn học tốt!!!
a) -x2y. 2xy3 = -2x3y4. Đơn thức có bậc là 7
b) x3y. (-2x3y5) = -2x6y6. Đơn thức có bậc là 12

a/ \(\left|x+\dfrac{3}{4}\right|-\dfrac{1}{3}=0\)
\(\Leftrightarrow\left|x+\dfrac{3}{4}\right|=\dfrac{1}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{3}{4}=\dfrac{1}{3}\\x+\dfrac{3}{4}=-\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5}{12}\\x=-\dfrac{13}{12}\end{matrix}\right.\)
Vậy ..............
b, \(\dfrac{-12}{-37}=\dfrac{12}{37}< \dfrac{12}{36}=\dfrac{13}{39}< \dfrac{13}{38}\)
\(\Leftrightarrow\dfrac{13}{38}>\dfrac{-12}{-37}\)
a)\(\text{|}x+\dfrac{3}{4}\text{|}-\dfrac{1}{3}=0\)
=>\(\text{|}x+\dfrac{3}{4}\text{|}=\dfrac{1}{3}\)
=>\(x+\dfrac{3}{4}=-\dfrac{1}{3}\)hoặc\(x+\dfrac{3}{4}=\dfrac{1}{3}\)
=>\(x=-\dfrac{13}{12}\)hoặc\(x=-\dfrac{5}{12}\)
Vậy...
b)\(\dfrac{13}{38}\) và \(\dfrac{-12}{-37}\)
Ta có:\(\dfrac{-12}{-37}=\dfrac{12}{37}< \dfrac{12}{36}=\dfrac{1}{3}=\dfrac{13}{39}< \dfrac{13}{38}\)
=>\(\dfrac{13}{38}>\dfrac{-12}{-37}\)

#)Giải :
\(A=\left(1-\frac{z}{y}\right).\left(1-\frac{x}{y}\right).\left(1-\frac{y}{z}\right)\)
\(A=\frac{x-z}{x}.\frac{x+y}{z}.\frac{z-y}{x}\)
\(x+y-z=0\Leftrightarrow\hept{\begin{cases}x+y=z\\x-z=-y\\z-y=x\end{cases}}\)
Thay vào A, ta được :
\(A=\frac{-y}{x}.\frac{z}{y}.\frac{x}{z}=\frac{-yzx}{xyz}=-1\)
~Will~be~Pens~

\(x+y=0\Rightarrow x=-y\)
\(M=x^3-xy^2+x^2y-y^3-1\)
\(M=\left(-y\right)^3-\left(-y\right)\cdot y^2+\left(-y\right)^2y-y^3-1\)
\(M=\left(-y\right)^3-\left(-y\right)^3+y^3-y^3-1\)
\(\Rightarrow M=-1\)
Ta có:
M = x3 - xy2 + x2y - y3 - 1
M =( x3 + x2y) - ( xy2 + y3) - 1
M = x2( x + y) - y2 ( x + y) - 1
M = x2.0 - y2.0 - 1
M = 0 - 0 - 1
M = -1
Vậy M = -1
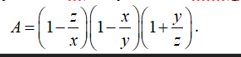

\(x-y-z=0\Leftrightarrow\left\{{}\begin{matrix}x-z=y\\y-x=-z\\y+z=x\end{matrix}\right.\)
\(A=\left(1-\dfrac{z}{x}\right)\left(1-\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)=\dfrac{x-z}{x}.\dfrac{y-x}{y}.\dfrac{y+z}{z}=\dfrac{y}{x}.\dfrac{-z}{y}.\dfrac{x}{z}=-1\)