Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(B=\frac{ab}{a+b+2}\Rightarrow2B=\frac{2ab}{a+b+2}=\frac{\left(a+b\right)^2-a^2-b^2}{a+b+2}=\frac{\left(a+b\right)^2-4}{a+b+2}=a+b-2\)
Do a ; b không âm , áp dụng BĐT Cô - si cho 2 số , ta có :
\(a+b\le\sqrt{2\left(a^2+b^2\right)}=\sqrt{2.4}=\sqrt{8}\)
\(\Rightarrow a+b-2\le\sqrt{8}-2\)
\(\Rightarrow2B\le\sqrt{8}-2\Rightarrow B\le\sqrt{2}-1\)
Dấu " = " xảy ra \(\Leftrightarrow a=b=\sqrt{2}\)
Do x ; y không âm , \(x^2+y^2=1\)
\(\Rightarrow\left|x\right|;\left|y\right|\le1\) \(\Rightarrow0\le x;y\le1\)
\(\Rightarrow x\ge x^2;y\ge y^2\Rightarrow x+y\ge x^2+y^2=1\)
\(x,y\ge0\Rightarrow xy\ge0\)
Ta có : \(A=\sqrt{5x+4}+\sqrt{5y+4}\)
\(\Rightarrow A^2=5x+4+5y+4+2\sqrt{\left(5x+4\right)\left(5y+4\right)}\)
\(=5\left(x+y\right)+8+2\sqrt{25xy+20y+20x+16}\)
\(\ge5.1+8+2\sqrt{25.0+20.1+16}=13+2.6=25\)
\(\Rightarrow A\ge5\)
Dấu " = " xảy ra \(\Leftrightarrow\left[{}\begin{matrix}x=0;y=1\\x=1;y=0\end{matrix}\right.\)

\(\Leftrightarrow p=\left(xy\right)^4+1+x^4+y^4\)ap dung bat dang thuc cosi
\(\Leftrightarrow p\ge4\left(xy\right)^2vi\left(xy\right)^2\ge0\Rightarrow\)p nho nhat

Ta có : \(\left(x-y\right)^2\ge0\Leftrightarrow x^2+y^2\ge2xy\Leftrightarrow2\left(x^2+y^2\right)\ge x^2+2xy+y^2\)
\(\Leftrightarrow x^2+y^2\ge\frac{1}{2}\left(x+y\right)^2=\frac{1}{2}.10=5\)
Vậy MIN P = 5 khi x = y = \(\frac{\sqrt{10}}{2}\)

Ta chứng minh được:
\(0\le x:y\le1\)
\(\Rightarrow x\ge x^2;y\ge y^2;xy\ge0\)
\(P^2=8+5\left(x+y\right)+2\sqrt{16+20\left(x+y\right)+25xy}\)
\(P^2\ge8+5\left(x^2+y^2\right)+2\sqrt{16+20\left(x^2+y^2\right)}\)
\(P^2\ge8+5+2\sqrt{16+20}=25\)
\(\Rightarrow P\ge5\)
Dấu "=" xảy ra \(\Leftrightarrow\orbr{\begin{cases}x=0;y=1\\x=1;y=0\end{cases}}\)

1. Ta có: \(x^2-2xy-x+y+3=0\)
<=> \(x^2-2xy-2.x.\frac{1}{2}+2.y.\frac{1}{2}+\frac{1}{4}+y^2-y^2-\frac{1}{4}+3=0\)
<=> \(\left(x-y-\frac{1}{2}\right)^2-y^2=-\frac{11}{4}\)
<=> \(\left(x-2y-\frac{1}{2}\right)\left(x-\frac{1}{2}\right)=-\frac{11}{4}\)
<=> \(\left(2x-4y-1\right)\left(2x-1\right)=-11\)
Th1: \(\hept{\begin{cases}2x-4y-1=11\\2x-1=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=0\\y=-3\end{cases}}\)
Th2: \(\hept{\begin{cases}2x-4y-1=-11\\2x-1=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=3\end{cases}}\)
Th3: \(\hept{\begin{cases}2x-4y-1=1\\2x-1=-11\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-5\\y=-3\end{cases}}\)
Th4: \(\hept{\begin{cases}2x-4y-1=-1\\2x-1=11\end{cases}}\Leftrightarrow\hept{\begin{cases}x=6\\y=3\end{cases}}\)
Kết luận:...

\(x^3+y^3+xy=x^2+y^2\)
\(\Leftrightarrow\left(x+y-1\right)\left(x^2-xy+y^2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+y=1\\x^2-xy+y^2=0\end{cases}}\)
- \(x^2-xy+y^2=0\Rightarrow x=y=0\Rightarrow P=\frac{5}{2}\).
- \(x+y=1\Rightarrow0\le x,y\le1\).
\(P=\frac{1+\sqrt{x}}{2+\sqrt{y}}+\frac{2+\sqrt{x}}{1+\sqrt{y}}\ge\frac{1}{2+\sqrt{y}}+\frac{2}{1+\sqrt{y}}\ge\frac{1}{2+1}+\frac{2}{1+1}=\frac{4}{3}\)
Dấu \(=\)xảy ra tại \(x=0,y=1\).
\(P=\frac{1+\sqrt{x}}{2+\sqrt{y}}+\frac{2+\sqrt{x}}{1+\sqrt{y}}\le\frac{1+\sqrt{x}}{2}+\frac{2+\sqrt{x}}{1}\le\frac{1+1}{2}+\frac{2+1}{1}=4\)
Dấu \(=\)xảy ra tại \(x=1,y=0\).
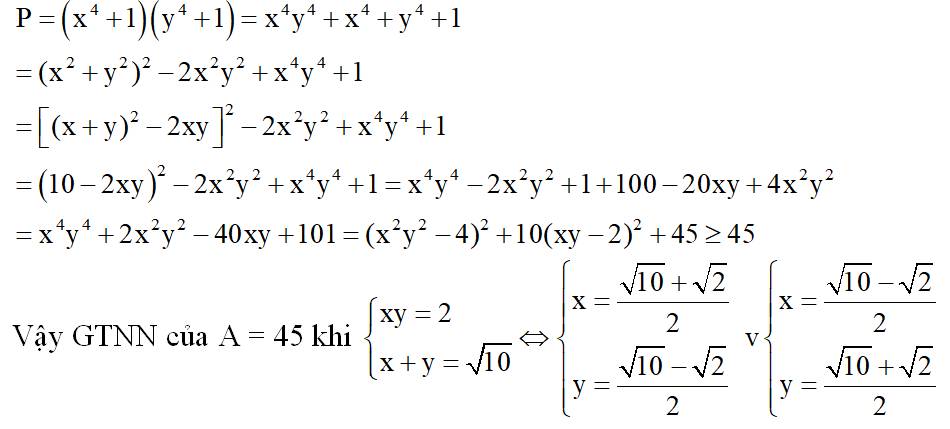
Do \(x^2+y^2=1\Rightarrow0\le x;y\le1\)
\(\Rightarrow\left\{{}\begin{matrix}x^2\le x\\y^2\le y\end{matrix}\right.\) \(\Rightarrow x+y\ge x^2+y^2=1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{4+5x}=a\\\sqrt{4+5y}=b\end{matrix}\right.\) \(\left\{{}\begin{matrix}2\le a;b\le3\\a^2+b^2=8+5\left(x+y\right)\ge13\end{matrix}\right.\)
Do \(2\le a;b\le3\Rightarrow\left\{{}\begin{matrix}\left(a-2\right)\left(a-3\right)\le0\\\left(b-2\right)\left(b-3\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2-5a+6\le0\\b^2-5b+6\le0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a\ge\frac{a^2+6}{5}\\b\ge\frac{b^2+6}{5}\end{matrix}\right.\)
\(\Rightarrow P=a+b\ge\frac{a^2+6}{5}+\frac{b^2+6}{5}=\frac{a^2+b^2+12}{5}\ge\frac{13+12}{5}=5\)
\(\Rightarrow P_{min}=5\) khi \(\left(a;b\right)=\left(2;3\right)\) và hoán vị hay \(\left(x;y\right)=\left(0;1\right)\) và hoán vị
Ủng hộ cách khác
Dễ cm: \(x\ge x^2;y\ge y^2\)
\(P=\sqrt{4+5x}+\sqrt{4+5y}=\sqrt{x+4x+4}+\sqrt{y+4y+4}\ge\sqrt{x^2+4x+4}+\sqrt{y^2+4y+4}=\left|x+2\right|+\left|y+2\right|=x+y+4\ge x^2+y^2+4=1\)"=" khi x;y là hoán vị của (0;1)