Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAHC vuông tại H và ΔAIC vuông tại I có
AC chung
góc HAC=góc IAC
=>ΔAHC=ΔAIC
=>AH=AI và CH=CI

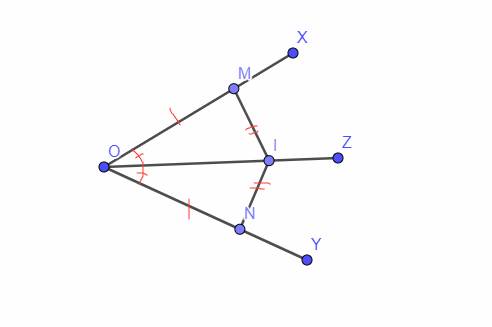
`a,` Xét Tam giác `OIM` và Tam giác `OIN` có:
`OM = ON (g``t)`
\(\widehat{MOI}=\widehat{NOI}\) `(` tia phân giác \(\widehat{xOy}\) `)`
`OI` chung
`=>` Tam giác `OIM =` Tam giác `OIN (c-g-c)`
`b,` Vì Tam giác `OIM =` Tam giác `OIN (a)`
`->` \(\widehat{OIM}=\widehat{OIN}\) `( 2` góc tương ứng `)`
`c,` Vì Tam giác `OIM =` Tam giác `OIN (a)`
`-> IM = IN (2` cạnh tương ứng `)`
`\color{blue}\text {#DuyNam}`

a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOAM=ΔOBM
=>MA=MB
Xét ΔMAF vuông tại A và ΔMBE vuông tại B có
MA=MB
\(\widehat{AMF}=\widehat{BME}\)
Do đó: ΔMAF=ΔMBE
=>MF=ME
b:
Ta có: OA=OB
=>O nằm trên đường trung trực của BA(1)
Ta có: MA=MB
=>M nằm trên đường trung trực của BA(2)
Từ (1) và (2) suy ra OM là đường trung trực của BA
=>OM\(\perp\)BA


b) Xét tam giác AOC và tam giác BOC có:OA=OB(gt)góc AOC = góc BOC(OC là tia phân giác góc AOB)OC chung=>tam giác AOC=tam giác BOC(c-g-c)=>góc OAC= góc OBC=90độ(2 góc tương ứng)=>BC vuông góc với Ox

Xét ΔOAB có
AM là phân giác góc ngoài tại A
BM là phân giác góc ngoài tại B
=>OM là phân giác của góc xOy
=>M cách đều hai cạnh của góc xOy