Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt AC = x; BD = y (x, y > 0)
Ta có \(\Delta ACM\sim\Delta BMD\left(g-g\right)\Rightarrow\frac{AC}{MB}=\frac{AM}{BD}\)
\(\Rightarrow AC.BD=AM.MB=const\Rightarrow xy=c=const\)
\(S_{MCD}=S_{ACDB}-S_{ACM}-S_{MBD}=\frac{\left(x+y\right)\left(AM+MB\right)}{2}-\frac{x.AM}{2}-\frac{y.MB}{2}\)
\(=\frac{x.MB+y.AM}{2}\ge\sqrt{xy.MB.AM}=\sqrt{c^2}=c\)
Dấu bằng xảy ra khi x.MB = y.AM, lại có \(xy=MB.AM\Rightarrow\hept{\begin{cases}x=AM\\y=MB\end{cases}}\)
Vậy giá trị nhỏ nhất của \(S_{CMD}=c\left(đvdt\right)\) xảy ra khi AC = AM; BD = BM.

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Linhllinh - Toán lớp 9 - Học toán với OnlineMath

* Phân tích
Giả sử đường tròn (I) dựng được thỏa mãn điều kiện bài toán
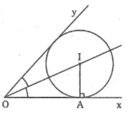
- Đường tròn (I) tiếp xúc với Ox và Oy nên điểm I nằm trên tia phân giác của góc xOy
- Đường tròn (I) tiếp xúc với Ox tại A nên I nằm trên đường vuông góc với Ox kẻ từ A
Vậy I là giao điểm của tia phân giác góc xOy và đường thẳng vuông góc với Ox tại A
* Cách dựng
- Dựng tia phân giác của góc xOy
- Dựng đường thẳng vuông góc với Ox tại A cắt tia phân giác của góc xOy tại I
- Dựng đường tròn (I; IA)
* Chứng minh
Ta có: Ox ⊥ IA tại A nên Ox là tiếp tuyến của (I)
I nằm trên tia phân giác của góc xOy nên I cách đều hai cạnh Ox, Oy. Khi đó khoảng cách từ I đến Oy bằng IA nên Oy cũng là tiếp tuyến của đường tròn (I).
Vậy đường tròn (I) đi qua A và tiếp xúc với hai cạnh của góc xOy.
* Biện luận
Vì góc xOy nhỏ hơn 180 ° nên góc tạo bởi một cạnh của góc với tia phân giác là góc nhọn. Khi đó đường thẳng vuông góc với Ox tại A luôn cắt tia phân giác của góc xOy.
trong nâng cao và phát triển có bài này thật đấy