Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
BD//AC
=>\(\widehat{DBA}=\widehat{BAC}\)(hai góc so le trong)(1)
CB//AD
=>\(\widehat{CBA}=\widehat{DAB}\)(hai góc so le trong)(2)
AB là phân giác của góc CAD
=>\(\widehat{CAB}=\widehat{DAB}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{DBA}=\widehat{CBA}\)
Xét ΔACB và ΔADB có
\(\widehat{DBA}=\widehat{CBA}\)
BA chung
\(\widehat{CAB}=\widehat{DAB}\)
Do đó: ΔACB=ΔADB
=>AC=AD và BC=BD
b: Xét ΔAHB vuông tại H và ΔAKB vuông tại K có
AB chung
\(\widehat{HAB}=\widehat{KAB}\)
Do đó: ΔAHB=ΔAKB
=>BH=BK
c: Xét tứ giác AHBK có
\(\widehat{AHB}+\widehat{AKB}+\widehat{KAH}+\widehat{KBH}=360^0\)
=>\(\widehat{KBH}+60^0+90^0+90^0=360^0\)
=>\(\widehat{KBH}=360^0-90^0-90^0-60^0=120^0\)

a: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
\(\widehat{BAD}=\widehat{CAD}\)
Do đó: ΔABD=ΔACD
=>AB=AC và DB=DC
Xét ΔABC có AB=AC
nên ΔABC cân tại A
b: Ta có: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: DB=DC
=>D nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AD là đường trung trực của BC
c: Xét ΔDBN vuông tại B và ΔDCM vuông tại C có
DB=DC
\(\widehat{BDN}=\widehat{CDM}\)(hai góc đối đỉnh)
Do đó: ΔDBN=ΔDCM
d: Ta có: ΔDBN=ΔDCM
=>DN=DM và BN=CM
Ta có: AB+BN=AN
AC+CM=AM
mà AB=AC và BN=CM
nên AN=AM
=>A nằm trên đường trung trực của NM(3)
ta có: DM=DN
=>D nằm trên đường trung trực của MN(4)
Từ (3) và (4) suy ra AD là đường trung trực của MN
Xét ΔAMN có \(\dfrac{AB}{BN}=\dfrac{AC}{CM}\)
nên BC//MN

a:
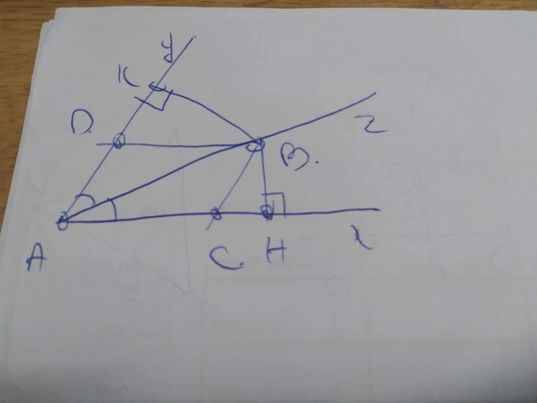
b:
BD//AC
=>\(\widehat{DBA}=\widehat{BAC}\)(hai góc so le trong)(1)
CB//AD
=>\(\widehat{CBA}=\widehat{DAB}\)(hai góc so le trong)(2)
AB là phân giác của góc CAD
=>\(\widehat{CAB}=\widehat{DAB}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{DBA}=\widehat{CBA}\)
Xét ΔACB và ΔADB có
\(\widehat{DBA}=\widehat{CBA}\)
BA chung
\(\widehat{CAB}=\widehat{DAB}\)
Do đó: ΔACB=ΔADB
=>AC=AD và BC=BD
c: Xét ΔAHB vuông tại H và ΔAKB vuông tại K có
AB chung
\(\widehat{HAB}=\widehat{KAB}\)
Do đó: ΔAHB=ΔAKB
=>BH=BK
d: Xét tứ giác AHBK có
\(\widehat{AHB}+\widehat{AKB}+\widehat{KAH}+\widehat{KBH}=360^0\)
=>\(\widehat{KBH}+60^0+90^0+90^0=360^0\)
=>\(\widehat{KBH}=360^0-90^0-90^0-60^0=120^0\)