Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : xy-3x+2z=10
=> xy-3x+2z-4=6
ta xét : (x2+y2+z2)-(xy-3x+2z-4) =0
=> x2+y2+z2-xy+3x-2z+4=0
=> ( y2-xy+\(\dfrac{x^2}{4}\)) + (\(\dfrac{3x^2}{4}\)+3x+3) + (z2-2z+1)=0
=> \(\dfrac{\left(2y-x\right)^2}{4}\)+ \(\dfrac{3}{4}\)(x2+4x+4) + (z-1)2 =0
=> \(\dfrac{\left(2y-x\right)^2}{4}\) + \(\dfrac{3\left(x+2\right)^2}{4}\) + (z-1)2=0
ta thấy cả biểu thức trên đều lớn hơn hoặc bằng 0 với mọi x,y,z ( tự lí luận)
do đó : \(\dfrac{\left(2y-x\right)^2}{4}\)+\(\dfrac{3\left(x+2\right)^2}{4}\)+ (z-1)2=0 khi và chỉ khi z=1,x=-2,y=-1 .
thay z=1,x=-2,y=-1 vào P ta được :
P=2020
Chúc bạn học giốt !@@@

Bạn CM x=y=z=1
Sau đó bạn thế số vào và bạn sẽ tính đc phân số là 3/6 rút gọn là 1/2
Cuối cùng bạn sẽ kết luận:
Vì 1/2 ≤ 1/2
Nên ...(biểu thức)...≤1/2

a: x-y-z=0
=>x=y+z; y=x-z; z=x-y
\(K=\dfrac{x-z}{x}\cdot\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}=\dfrac{y\cdot\left(-z\right)\cdot x}{xyz}=-1\)
b: Tham khảo:
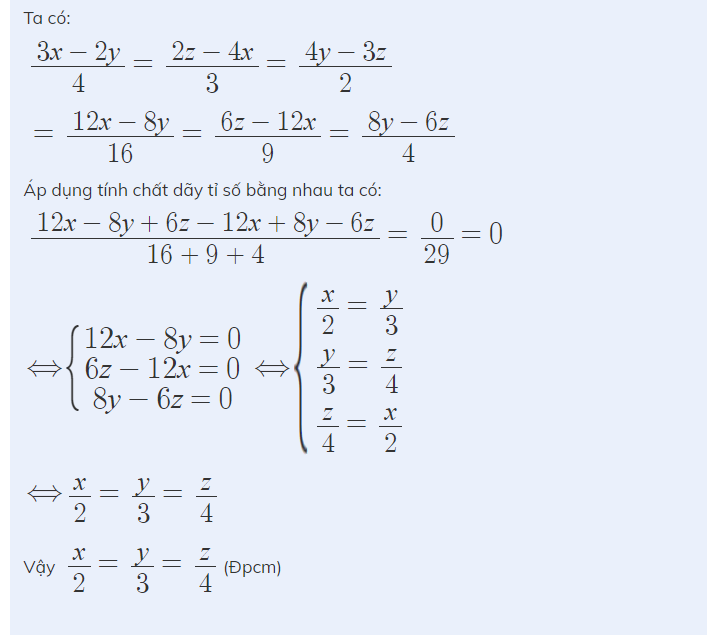

\(yz\left(y+z\right)+zx\left(z-x\right)-xy\left(x+y\right)\)
\(=yz\left(y+z\right)+zx\left(z-x\right)-xy\left[\left(y+z\right)-\left(z-x\right)\right]\)
\(=yz\left(y+z\right)+zx\left(z-x\right)-xy\left(y+z\right)+xy\left(z-x\right)\)
\(=y\left(y+z\right)\left(z-x\right)+x\left(z-x\right)\left(z-y\right)\)
\(=\left(z-x\right)\left(yz-xy+xz-xy\right)\)

6) Ta có
\(A=\frac{x^3}{y+2z}+\frac{y^3}{z+2x}+\frac{z^3}{x+2y}\)
\(=\frac{x^4}{xy+2xz}+\frac{y^4}{yz+2xy}+\frac{z^4}{zx+2yz}\)
\(\ge\frac{\left(x^2+y^2+z^2\right)^2}{xy+2xz+yz+2xy+zx+2yz}\)
\(\Leftrightarrow A\ge\frac{1}{3\left(xy+yz+zx\right)}\ge\frac{1}{3\left(x^2+y^2+z^2\right)}=\frac{1}{3}\)
