Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án : A
Gọi số có 3 chữ số là 
Có 9 cách chọn số a từ tập X.
Có 8 cách chọn số b vì b khác a.
Có 7 cách chọn số c vì c khác a; c khác b.
Vậy theo quy tắc nhân; có 9.8.7= 504 số thỏa mãn.
Đáp án : D
Do số cần lập là số chẵn nên có 4 cách chọn chữ sỗ c từ tập X; c ∈ {2;4;6;8}.
Ứng với mỗi cách chọn c ta có 8 cách chọn a- vì a khác c.
Khi đó; có 7 cách chọn b vì b khác a; b khác c.
Vậy từ quy tắc nhân có 4.8.7=224 số thỏa mãn.
Phương án 1: Chữ số hàng trăm là 1.
Khi đó có 8 cách chọn chữ số hàng chục và 7 cách chọn chữ số hàng đơn vị thỏa mãn đề bài.
Theo quy tắc nhân có 8.7=56 số thỏa mãn.
· Phương án 2: Chữ số hàng chục là 1.
Khi đó có 8 cách chọn chữ số hàng trăm và 7 cách chọn chữ số hàng đơn vị thỏa mãn đề bài.
Theo quy tắc nhân có 8.7=56 số thỏa mãn.
· Phương án 3: chữ số hàng đơn vị là 1.
Khi đó có 8 cách chọn chữ số hàng trăm và 7 cách chọn chữ số hàng chục.
Theo quy tắc nhân có 8.7=56 số thỏa mãn.
Vậy theo quy tắc cộng; có 56+56+56=168 số thỏa mãn.
Chọn A.
Phương án 1: chữ số hàng trăm là 4; chữ số hàng chục là 9 thì chỉ có 2 số là 491 và 492; 493; 495
Phương án 2: chữ sỗ hàng trăm là 4; chữ số hàng chục khác 9. Khi đó; có 7 cách chọn chữ số hàng chục từ tập X ( chữ số hàng chục thuộc {1;2;3;5;6;7;8} ứng với mỗi cách chọn chữ số hàng chục có 7 cách chọn chữ số hàng đơn vị.
Theo quy tắc nhân có 1.7.7=49 cách thỏa mãn phương án này.
Phương án 3: chữ số cần lập nhỏ hơn 400. Có 3 cách chọn chữ số hàng trăm; ứng với mỗi cách chọn chữ số hàng trăm có 8 cách chọn chữ số hàng chục và 7 cách chọn chữ số hàng đơn vị.
Theo quy tắc nhân; có 3.8.7=168 số thỏa mãn phương án này.
Vậy từ quy tắc cộng có: 4+49+168=221 số thỏa mãn.
Chọn A.
Đáp án : A
+) 
; c có 4 cách chọn. Chọn chữ số còn lại có 7 cách chọn.
+) 
; c có 3 cách chọn. Chọn chữ số còn lại có 7 cách chọn.
+) a = 7; 
; b khác 9, b có 6 cách chọn.
+) a = 7; c = 8; b có 6 cách chọn
Vậy có 3.4.7 + 3.3.7 + 3.6 + 6 = 171 số.
Đáp án : D
Để tính nhanh với bài này ta dùng quy tắc phần bù.
Trước tiên ta tính số các số chẵn có 5 chữ số đôi một khác nhau và được lập ra từ các chữ số của tập A.
+ Gọi các số đó là 
e có 4 cách chọn( vì x là số chẵn nên e có thể là 2;34;6;8); a có 8 cách; b có 7 cách; c có 6 cách và d có 5 cách.
Nên có tất cả 4.8.7.6.5=6720 số
+ Gọi 
là số bắt đầu bởi 125 và có 5 chữ số đôi một khác nhau.
Suy ra b có 3 cách chọn (b có thể là 2;4;8), a có 5 cách chọn nên có số.
+ Suy ra có tất cả 6720 - 15 = 6705 số cần tìm.
Đáp án D
Ta có bộ 3 số có tổng chia hết cho 3 là: {1;2;3}, {1;2;6}, {1;2;9}, {1;3;5}, {1;3;8}, {1;4;7}, {1;5;6},{1;5;9}, {1;6;8}, {1;8;9}, {2;3;4}, {2;3;7}, {2;4;6}, {2;4;9}, {2;5;8}, {2;6;7}, {2;7;9}, {3;4;5}, {3;4;8}, {3;5;7}, {3;6;9}, {3;7;8}, {4;5;6}, {4;5;9}, {4;6;8}, {5;6;7}, {6;7;8}, {7;8;9}.
Mỗi bộ số ta lập được 3! = 6 số.
Vậy có 30.6=180 số.
Đề có yêu cầu gì về các chữ số phân biệt hay không nhỉ?
Đáp án : B
Gọi số có 3 chữ số là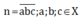
Có 9 cách chọn chữ số a từ tập X.
Có 9 cách chọn chữ số b từ tập X.
Có 9 cách chọn chữ số c từ tập X.
Vậy theo quy tắc nhân có 9.9.9=729 số thỏa mãn.