Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(x+3y=t\) thì biểu thức được viết lại dưới dạng biến \(t\) như sau:
\(t^3-6t^2+12t=-19\)
\(\Leftrightarrow\) \(t^3-6t^2+12t+19=0\)
\(\Leftrightarrow\) \(\left(t-1\right)\left(t^2-7t+19\right)=0\) \(\left(a\right)\)
Mà \(t^2-7t+19=\left(t-\frac{7}{2}\right)^2+6\frac{3}{4}>0\) với mọi \(t\)
nên từ \(\left(a\right)\) \(\Rightarrow\) \(t=1\), tức là \(x+3y=1\)

\(3y-x=6\) => \(x=3y-6\)
Thay \(x=3y-6\) vào biểu thức A. Ta có:
\(A=\left(\frac{3y-6}{y-2}\right)+\left(\frac{2\left(3y-6\right)-3y}{3y-6-6}\right)=\left(\frac{3\left(y-2\right)}{y-2}\right)+\left(\frac{6y-12-3y}{3y-12}\right)\)
\(A=\left(\frac{3\left(y-2\right)}{y-2}\right)+\left(\frac{3y-12}{3y-12}\right)=3+1=4\)

Bài này quá dễ:vv
Ta có 3y-x=6
=> \(\left\{{}\begin{matrix}3y=6+x\\x=3y-6\end{matrix}\right.\)
Thay vào A ta có: \(A=\dfrac{x}{y-2}+\dfrac{2x-3y}{x-6}=\dfrac{3y-6}{y-2}+\dfrac{2x-6-x}{x-6}=\dfrac{3\left(y-2\right)}{y-2}+\dfrac{x-6}{x-6}=3+1=4\)Vậy khi 3y-x=6 thì A=4

Lời giải:
Sửa đề đoạn $x-3y$ thành $x+3y$
$A=x^3+(3y)^3+3y(x^2-9y^2)-(3x^2y+7x^2-7x)$
$=x^3+27y^3+3x^2y-27y^3-3x^2y-7x^2+7x$
$=x^3-7x^2+7x$ không phụ thuộc vào giá trị của biến $y$ (đpcm).
b.
Khi $x=-1$ thì:
$A=(-1)^3-7(-1)^2+7(-1)=-1-7-7=-15$

- áp dụng hằng đẳng thức (x+3y)3-6(x+3y)2+12(x+3y)=-19
x3+3x23y+3x3y
đéo giải nửa án lớn bỏ đi con
Đặt x + 3y = a, ta có:
a3 - 6a2 +12a = -19
=> a3 - 6a2 +12a +19 = 0
=> a3 +a2 - 7a2 - 7a +19a +19 =0
=> a2(a +1) - 7a(a +1) +19(a+1) =0
=> (a2 -7a +19)(a +1)=0
=> a + 1 = 0 ( Vì a2 -7a +19 > 0 với mọi a)
=> a = -1
=> x + 3y = -1
Vậy: x + 3y = -1

\(A=(x+3y)(x^2-3xy+9y^2)+3y(x+3y)(x-3y)-x(3xy+x^2-5)-5x+1\\A=(x+3y)[x^2-x\cdot3y+(3y)^2]+3y[x^2-(3y)^2]-3x^2y-x^3+5x-5x+1\\A=x^3+(3y)^3+3y(x^2-9y^2)-3x^2y-x^3+1\\A=x^3+27y^3+3x^2y-27y^3-3x^2y-x^3+1\\A=1\)$\Rightarrow$ Giá trị của $A$ không phụ thuộc vào giá trị của biến.

Ta có : \(x^2+3y^2=4xy\)
\(\Leftrightarrow\left(x^2-xy\right)+\left(3y^2-3xy\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x-3y\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=y\\x=3y\end{cases}}\)
Với \(x=y\) thì \(A=\frac{2x+3x}{x-2x}=-5\)
Với \(x=3y\) thì \(A=\frac{6y+3y}{3y-2y}=9\)
Ta có:
\(x^2+3y^2=4xy\Leftrightarrow\left(x^2-3xy\right)-\left(xy-3y^2\right)=0\Leftrightarrow\left(x-3y\right)\left(x-y\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=3y\\x=y\end{cases}}\)
TH1: x=3y
\(A=\frac{6y+3y}{3y-2y}=\frac{9y}{y}=9\)
TH2: x=y
\(A=\frac{2x+3x}{x-2x}=\frac{5x}{-x}=-5\)
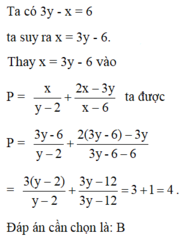
\(\Leftrightarrow\left(x+3y\right)^3-6\left(x+3y\right)^2+12\left(x+3y\right)-8=-27\)
\(\Leftrightarrow\left(x+3y-2\right)^3=-27\)
\(\Leftrightarrow\left(x+3y-2\right)^3=\left(-3\right)^3\)
\(\Rightarrow x+3y-2=-3\)
\(\Rightarrow x+3y=-1\)