Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

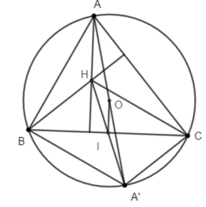
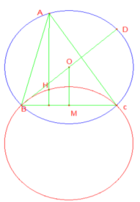
Gọi A’ là điểm đối xứng với A qua O. Ta có: BH // A’C suy ra BHCA’ là hình bình hành do đó HA’ cắt BC tại trung điểm I của BC. Mà O là trung điểm của AA’ suy ra OI là đường trung bình của tam giác AHA’ suy ra A H → = 2 O I →
Chọn đáp án C

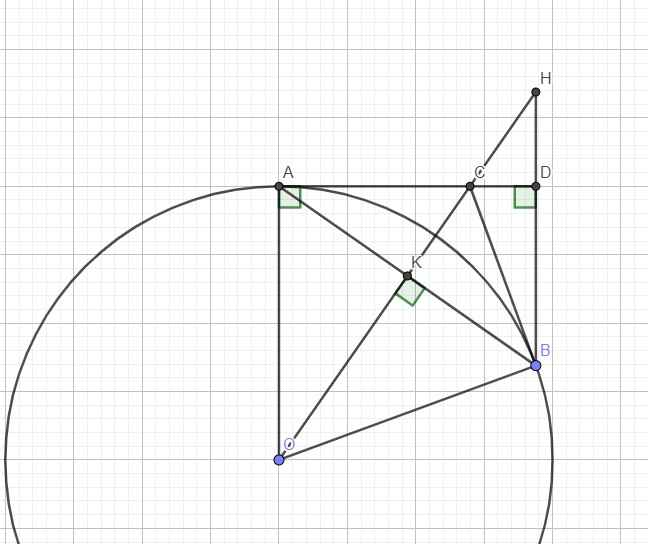
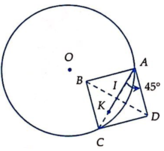
Theo tính chất 2 tiếp tuyến cắt nhau ta có \(AC=BC\)
Mặt khác \(OA=OB=R\)
\(\Rightarrow OC\) là trung trực AB hay \(OC\perp AB\)
\(\Rightarrow\Delta AOK\) vuông tại K
\(\Rightarrow\) Tập hợp K là đường tròn (C) đường kính AO cố định
b.
Do H là trực tâm \(\Rightarrow BH\perp AD\Rightarrow BH||AO\) (cùng vuông góc AD)
\(\Rightarrow\widehat{OAK}=\widehat{KBH}\) (so le trong)
Mà \(AK=BK\) (OC là trung trực AB)
\(\Rightarrow\Delta_VOAK=\Delta_VKBH\left(g.c.g\right)\)
\(\Rightarrow OK=KH\) hay K là trung điểm OH
\(\Rightarrow\overrightarrow{OH}=2\overrightarrow{OK}\Rightarrow H\) là ảnh của K qua phép vị tự tâm O tỉ số \(k=2\)
\(\Rightarrow\) Tập hợp H là đường tròn ảnh của (C) qua phép vị tự tâm O tỉ số \(k=2\) (với (C) là đường tròn đã xác định ở câu a)

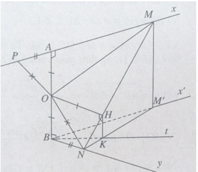
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
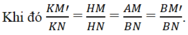
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK). Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β). Trong mặt phẳng (β) ta có OH = a. Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)

Bạn lấy thực hiện phép đối xứng qua \(BC\) thì \(O\) thành \(O'\) thì \(OB=O'B,OC=O'C\) mà \(OB=C=R\) cho nên \(O'B=O'C=R\left(1\right)\)
Ở đây \(R\) là bán kính đường tròn ngoại tiếp \(ABC'\)
, \(H\) thành \(H'\) với \(O\) là tâm đường tròn ngoại tiếp \(ABC\).
Cho nên \(\widehat{HBC}=\widehat{H'BC}\) ( phép đối xứng trực bảo toàn góc) mặt khác
\(\widehat{HBC}=\widehat{HAC}\) cùng phụ với góc \(\widehat{C}\).
Điều này chứng tỏ \(ACH'B\) là tứ giác nội tiếp hay \(H'\) cũng thuộc \(\left(O\right)\)
Phép đối xứng là phép dời hình cho nên nó bảo toàn khoảng cách cũng có nghĩa
\(O'H=OH'=R\) (vì \(H\) nằm trên \(\left(O\right)\)) (2)
Từ (1) và (2) ta được tam giác HBC luôn nội tiếp đường tròn \(\left(O'\right)\) bán kính R
do \(O,BC\) và R cố định nên \(O'\) cố định , ta được điều phải chứng minh.