Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

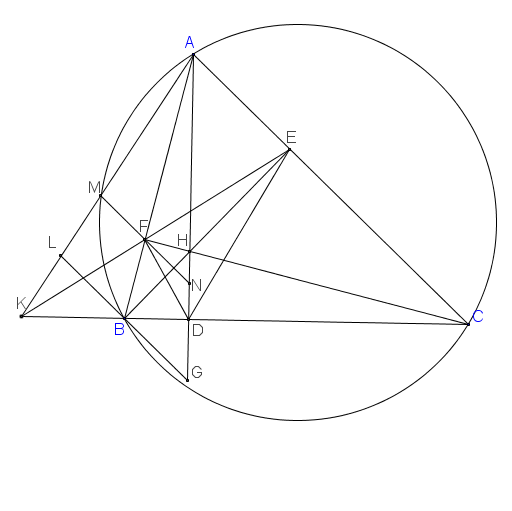
Xét $(O)$ có: $\widehat{ACD}=\widehat{ABD}=90^o$( góc nội tiếp chắn nửa đường tròn)
suy ra $\widehat{ECD}=90^o$
$\widehat{BAC}=\widehat{BDC}$ (các góc nội tiếp cùng chắn cung $BC$)
hay $\widehat{BAE}=\widehat{EDC}(1)$
Xét tứ giác $BEFA$ có: $\widehat{ABE}=\widehat{EFA}=90^o$ (do $EF AD$)
nên $\widehat{ABE}+\widehat{EFA}=180^o$
suy ra tứ giác $BEFA$ nội tiếp
suy ra $\widehat{EFB}=\widehat{BAE}(2)$ (các góc nội tiếp cùng nhắn $BE$)
Chứng minh tương tự ta có: tứ giác $ECDF$ nội tiếp nên $\widehat{EFC}=\widehat{EDC}(3)$ (các góc nội tiếp cùng chắn cung $EC$)
Từ $(1)(2)(3)$ suy ra $\widehat{EFB}+\widehat{EFC}=\widehat{BAE}+\widehat{EDC}=2.\widehat{EDC}$
hay $\widehat{BFC}=2.\widehat{EDC}$
Lại có: tam giác $ECD$ vuông tại $C$
$M$ là trung điểm $ED$
Nên $EM=MD=CM$
Suy ra tam giác $MCD$ cân tại $M$
nên $\widehat{MCD}=\widehat{MDC}$
Lại có: $\widehat{BMC}$ là góc ngoài tam giác $MCD$ nên
$\widehat{BMC}=\widehat{MCD}+\widehat{MDC}=2.\widehat{MDC}=2.\widehat{EDC}
Mà $\widehat{BFC}=2.\widehat{EDC}$
nên $\widehat{BMC}=\widehat{BFC}$
suy ra $F;M$ cùng nhìn đoạn $BC$ dưới 1 góc ko đổi
$F;M$ là 2 đỉnh liên tiếp tứ giác $BCMF$
suy ra tứ giác $BCMF$ nội tiếp (Bài toan quỹ tích cung chứa góc)

gọi M là trung điểm của AF . Ta có OM là đường trung bình của tam giác ACF
\(=>OM//CF,OM=\frac{1}{2}CF\)
ta lại có \(OM//CF,CF\perp CD\left(gt\right)\)
\(=>OM\perp CD.Mà\left(AB//CD\right)\)
\(=>OM//BE\)(1)
mặt khác OM , AM là 2 đường cao của tam giác ABO
=> M là trực tâm của tam giác ABO
=>\(BM\perp AC.Mà\left(EO\perp AC\right)=>BM//EO\left(2\right)\)
từ 1 zà 2 => tứ giác BMOE là hbh => OM=BE
ta có
\(OM=BE;OM=\frac{1}{2}CF=>BE=\frac{1}{2}CF\left(and\right)BE//OM//CF\)
\(\Delta KCF\)có \(CF//BE=>\frac{KE}{KF}=\frac{BE}{CF}=\frac{1}{2}\)

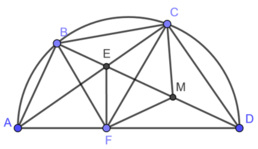
Xét tam giác vuông EFD có:
FM là đường trung tuyến ứng với cạnh huyền CD
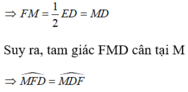
Ta có:
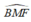 là góc ngoài tại đỉnh M của tam giác FMD nên:
là góc ngoài tại đỉnh M của tam giác FMD nên:

Xét tứ giác BCMF có:
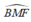 và
và 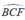 và cùng nhìn cạnh BF dưới một góc bằng nhau
và cùng nhìn cạnh BF dưới một góc bằng nhau
Suy ra, tứ giác BCMF nội tiếp được.

Tự vẽ hình nha ><
a) ^ABD = 900 => ^ABE = 900
EF \(\perp\)AD => ^EFA = 900
=> Tứ giác ABEF có tổng 2 góc đối = 900 nội tiếp được đường tròn