Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

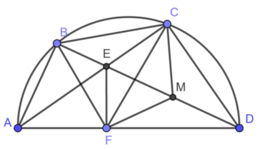
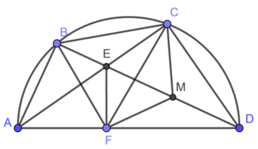
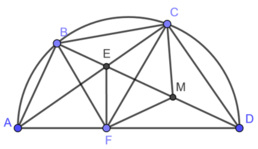
a) Xét (O) có
ΔACD nội tiếp đường tròn(A,C,D\(\in\)(O))
AD là đường kính(gt)
Do đó: ΔACD vuông tại C(Định lí)
Suy ra: AC\(\perp\)CD tại C
hay \(EC\perp CD\) tại C
Xét tứ giác ECDF có
\(\widehat{EFD}\) và \(\widehat{ECD}\) là hai góc đối
\(\widehat{EFD}+\widehat{ECD}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ECDF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

Ta có: ˆACD=900ACD^=900 (góc nội tiếp chắn nửa đường tròn đường kính AD)
Xét tứ giác DCEF có:
ˆACD=900ACD^=900 (cm trên)
ˆEFD=900EFD^=900 (vì EF⊥ADEF⊥AD (gt))
⇒ˆACD+ˆEFD=1800⇒ACD^+EFD^=1800
=> Tứ giác DCEF là tứ giác nội tiếp đường tròn (đpcm).
b) Vì tứ giác DCEF là tứ giác nội tiếp (chứng minh câu a)
⇒ˆC1=ˆD1⇒C1^=D1^ (góc nội tiếp cùng chắn cung EF) (1)
Mà ⇒ˆC2=ˆD1⇒C2^=D1^ (góc nội tiếp cùng chắn cung AB) (2)
Từ (1) và (2) ⇒ˆC1=ˆC2⇒C1^=C2^
⇒⇒ CA là tia phân giác của ˆBCFBCF^ (đpcm)
k đúng hộ

Xét tam giác vuông EFD có:
FM là đường trung tuyến ứng với cạnh huyền CD
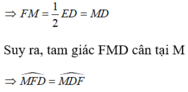
Ta có:
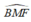 là góc ngoài tại đỉnh M của tam giác FMD nên:
là góc ngoài tại đỉnh M của tam giác FMD nên:

Xét tứ giác BCMF có:
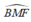 và
và 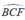 và cùng nhìn cạnh BF dưới một góc bằng nhau
và cùng nhìn cạnh BF dưới một góc bằng nhau
Suy ra, tứ giác BCMF nội tiếp được.

A D B C E H I O
Để chứng minh 5 điểm trên cùng thuộc một đường tròn, ta chứng minh góc BCH = góc BIH = góc BOH.
Thật vậy, theo chứng minh b, E là tâm đường tròn nội tiếp tam giác BCH nên CE là phân giác góc BCH. Từ đó góc BCH = 2 góc BCA.
Ta có góc BCA bằng góc BDA vì cùng chắn cung BA, nên góc BCH = 2 góc BDA (1)
Tam giác OBD cân tại O nên BOH = 2 góc BDA.(2)
Tam giác EHD vuông tại H , HI là trung tuyến ứng với cạnh huyền nên IH = ID, từ đó góc BIH = 2 góc BDA.(3)
Từ (1), (2), (3) ta suy ra 3 góc trên bằng nhau hay 5 điểm B, C, I, O, H cùng thuộc một đường tròn.

a: góc IED+góc ICD=180 độ
=>IEDC nội tiếp
b: góc ECI=góc BDA=1/2*sđ cung BA
=>góc ECI=góc BCI
=>CI là phân giác của góc BCE