Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

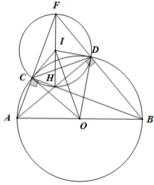
a) Vì C, D thuộc nửa đường tròn đường kính AB nên
A C B = A D B = 90 o ⇒ F C H = F D H = 90 o ⇒ F C H + F D H = 180 o
Suy ra tứ giác CHDF nội tiếp
b) Vì AH ⊥ BF, BH ⊥ AF nên H là trực tâm ∆ AFB ⇒ FH ⊥ AB
⇒ C F H = C B A ( = 90 o − C A B ) ⇒ Δ C F H ~ Δ C B A ( g . g ) ⇒ C F C B = C H C A ⇒ C F . C A = C H . C B

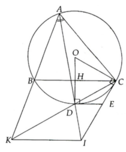
a, AD là phân giác B A C ^
=> D là điểm chính giữa B C ⏜ => OD ⊥ BC
Mà DE là tiếp tuyến => ĐPCM
b, E C D ^ = 1 2 s đ C D ⏜ = D A C ^ = B A D ^ => Đpcm
c, HC = P 3 2 => H O C ^ = 60 0 => B O C ^ = 120 0
=> l B C ⏜ = π . R . 120 0 180 0 = 2 3 πR
a) Ta có \(\widehat{DAB},\widehat{DCB}\) là 2 góc nội tiếp chắn nửa đường tròn\(\Rightarrow\widehat{DAB}=\widehat{DCB}=90^0\Rightarrow\widehat{DCI}=90^0\)
Xét tứ giác NICD có \(\widehat{DNI}+\widehat{DCI}=90^0+90^0=180^0\)
Suy ra tứ giác NICD nội tiếp
b) Xét △BCD và △BNI có
\(\widehat{DCB}=\widehat{BNI}\left(=90^0\right)\)
\(\widehat{B}\) chung
Suy ra △BCD \(\sim\) △BNI(g-g)\(\Rightarrow\frac{BC}{BN}=\frac{BD}{BI}\Rightarrow BN.BD=BI.BC\)