Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
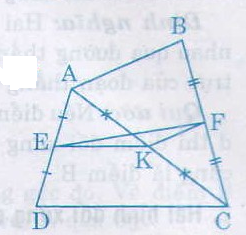
a) Trong ∆ACD có EA = ED, KA = KC (gt)
nên EK là đường trung bình của ∆ACD
Do đó EK = CD/2
Tương tự KF là đường trung bình của ∆ABC.
Nên KF = AB/2
b) Ta có EF ≤ EK + KF (bất đẳng thức trong ∆EFK)
Nên EF ≤ EK + KF = CD/2 + AB/2 = (AB+CD)/2
Vậy EF ≤ (AB+CD)/2
27. Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.
a) So sánh các độ dài EK và CD, KF và AB.
b) Chứng minh rằng EF \(\le\dfrac{AB+CD}{2}\)
Bài giải:
a) Trong ∆ACD có EA = ED, KA = KC (gt)
nên EK là đường trung bình của ∆ACD
Do đó EK =\(\dfrac{CD}{2}\)
Tương tự KF là đường trung bình của ∆ABC.
Nên KF = \(\dfrac{AB}{2}\)
b) Ta có EF ≤ EK + KF (bất đẳng thức trong ∆EFK)
Nên EF ≤ EK + KF = \(\dfrac{CD}{2}\) + \(\dfrac{AB}{2}\) = \(\dfrac{\left(AB+CD\right)}{2}\)
Vậy EF ≤ \(\dfrac{\left(AB+CD\right)}{2}\)
Xét ∆ EOM và ∆ FON có: ∠ (MEO) = ∠ (NFO) (so le trong do DE//BF)
OE = OF (tính chất hình bình hành)
∠ (MOE)= ∠ (NOF) (đối đỉnh )
Suy ra: ∆ EOM = ∆ FON (g.c.g) ⇒ OM = ON
Vậy tứ giác EMFN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường).
đố làm được ha
c: Ta có: \(EF\le KE+KF\)
\(\Leftrightarrow EF\le\dfrac{DC+AB}{2}\)
Dấu '='xảy ra khi E,K,F thẳng hàng
hay EF//AB//DC
Suy ra: ABCD là hình thang
a: Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
Suy ra: BF//DE
hay EM//FN
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Suy ra: AF//CE
hay MF//EN
Xét tứ giác EMFN có
EM//FN
EN//MF
Do đó: EMFN là hình bình hành
b: Ta có: AECF là hình bình hành
nên Hai đường chéo AC và EF cắt nhau tại trung điểm của mỗi đường(1)
Ta có: EMFN là hình bình hành
nên Hai đường chéo EF và MN cắt nhau tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra AC,EF,MN đồng quy