K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
30 tháng 11 2019
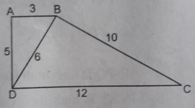
Chứng minh △ ABD ∼ △ BDC (c.c.c)
⇒ ∠ (ABD) = ∠ (BDC) ⇒ AB // CD.
15 tháng 1
a: Xét ΔABD và ΔBDC có
\(\dfrac{AB}{BD}=\dfrac{BD}{DC}=\dfrac{AD}{BC}\left(\dfrac{3}{6}=\dfrac{6}{12}=\dfrac{5}{10}\right)\)
Do đó: ΔABD~ΔBDC
b: Ta có: ΔABD~ΔBDC
=>\(\widehat{ABD}=\widehat{BDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//DC
=>ABCD là hình thang
CM
9 tháng 1 2019
a) Gợi ý: Lập tỉ số các cặp cạnh tương ứng và chứng minh chúng bằng nhau.
b) Từ phần a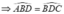 
Þ ĐPCM
6 tháng 3 2023
a: Xét ΔABD và ΔBDC có
AB/BD=BD/CD=AD/BC
=>ΔABD đồng dạng với ΔBDC
b: ΔABD đồng dạng với ΔBDC
=>góc ABD=góc BDC
=>AB//CD
VT
0
AB = 5cm
=> BC = 12 - 5 = 7cm
=> CD = 12 - 7 = 5cm
=> AD = 12 - 5 = 7cm
Vì AB = CD, BC = AD, mà AB đối CD, BC đối AD
=> Tứ giác ABCD là hbh