Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét tứ giác ABMD có
AB//MD
AB=MD
Do đó: ABMD là hình bình hành
mà AB=AD
nên ABMD là hình thoi
Ta có:
\(A-B=C-D\)
\(\Rightarrow A+D=B+C\)
Mặt khác:
\(A+B+C+D=360^o\)
\(\Rightarrow2\left(A+D\right)=360^o\left(A+D=B+C\right)\)
\(\Rightarrow A+D=180^o\)
Mà 2 góc có vị trí trong cùng phía
=> AB//CD
=> ABCD là hình thang
A-B=C-D
=>A-B+D-C=0
=>A+D-B-C=0
mà A+D+B+C=360
nên A+D=360/2=180
=>AB//CD
=>ABCD là hình thang
a: Xét tứ giác ABEF có
AF//BE
AF=BE
Do đó: ABEF là hình bình hành
mà AF=AB
nên ABEF là hình thoi
b: Đề sai rồi bạn
d: Xét tứ giác BMCD có
BM//CD
BM=CD
Do đó: BMCD là hình bình hành
Suy ra: Hai đường chéo BC và MD cắt nhau tại trung điểm của mỗi điểm
mà E là trung điểm của BC
nên E là trung điểm của MD
hay M,E,D thẳng hàng
Gọi E và F lần lượt là trung điểm của AC và BD; E' và F' lần lượt là hình chiếu của E, F trên đường thẳng m.
Khi đó, GG' là đường trung bình của hình thang EE'F'F
⇒ G G ' = 1 2 EE' +FF').
Mà EE' và FF' lần lượt là đường trung bình của hình thang AA'C'C và BB'D'D.
⇒ EE ' = 1 2 (AA' +CC') và FF ' = 1 2 (BB' +DD')
Thay vào (1) ta được ĐPCM
a) Gợi ý: Lập tỉ số các cặp cạnh tương ứng và chứng minh chúng bằng nhau.
b) Từ phần a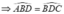
Þ ĐPCM