Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu b đề sai, hai mặt phẳng (SAC) và (SBD) không hề vuông góc với nhau (chúng chỉ vuông góc trong trường hợp ABCD là hình vuông)
Do câu b đề sai, (SAC) và (SBD) không vuông góc nên câu c rất khó tính :(
Từ A, kẻ \(AH\perp\left(SBD\right)\)
Gọi K là điểm đối xứng H qua O \(\Rightarrow\) AHCK là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm)
\(\Rightarrow\left\{{}\begin{matrix}CK//AH\\CK=AH\end{matrix}\right.\Rightarrow CK\perp\left(SBD\right)\) (K đương nhiên thuộc (SBD) do H, O đều thuộc (SBD))
\(\Rightarrow\widehat{CSK}\) là góc cần tìm
Trong mp (SBD), nối B và H kéo dài cắt SD tại E
\(\left\{{}\begin{matrix}SA\perp AB\\AB\perp AD\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\Rightarrow AB\perp SD\) (1)
Mà \(AH\perp\left(SBD\right)\Rightarrow AH\perp SD\) (2)
(1);(2) \(\Rightarrow SD\perp\left(ABE\right)\Rightarrow SD\perp AE\)
Áp dụng hệ thức lượng trong tam giác vuông SAD:
\(\frac{1}{AE^2}=\frac{1}{SA^2}+\frac{1}{AD^2}\)
Áp dụng hệ thức lượng trong tam giác vuông ABE:
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AE^2}=\frac{1}{AB^2}+\frac{1}{SA^2}+\frac{1}{AD^2}=\frac{1}{a^2}+\frac{1}{9a^2}+\frac{1}{4a^2}\Rightarrow AH=\frac{6a}{7}\)
Số đẹp quá ta :D
\(\Rightarrow CK=\frac{6a}{7}\)
Lại có:
\(SC=\sqrt{SA^2+AC^2}=\sqrt{SA^2+AB^2+BC^2}=a\sqrt{14}\)
\(\Rightarrow sin\widehat{CSK}=\frac{CK}{SC}=\frac{6}{7\sqrt{14}}\)

\(\left\{{}\begin{matrix}AO\perp OB\\AO\perp OC\end{matrix}\right.\) \(\Rightarrow AO\perp\left(ABC\right)\Rightarrow OA\perp BC\)
\(OH\perp\left(ABC\right)\Rightarrow OH\perp BC\)
\(\Rightarrow BC\perp\left(OAH\right)\)
b/ \(BC\perp\left(OAH\right)\Rightarrow BC\perp AH\Rightarrow AH\) là 1 đường cao trong tam giác ABC
Chứng minh tương tự câu a ta có\(AC\perp\left(OBH\right)\Rightarrow AC\perp BH\Rightarrow BH\) cùng là 1 đường cao
\(\Rightarrow H\) là trực tâm tam giác ABC
c/ Gọi M là giao điểm AH và BC \(\Rightarrow AM\perp BC\)
Áp dụng hệ thức lượng: \(\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OM^2}\) (2)
\(BC\perp\left(OAH\right)\Rightarrow BC\perp OM\Rightarrow OM\) là đường cao ứng với cạnh huyền trong tam giác vuông OBC
Áp dụng hệ thức lượng: \(\frac{1}{OM^2}=\frac{1}{OB^2}+\frac{1}{OC^2}\) (3)
(2);(3) \(\Rightarrow\) đpcm
d/ \(cosA=\frac{AB^2+AC^2-BC^2}{2AB.AC}=\frac{OA^2+OB^2+OA^2+OC^2-\left(OB^2+OC^2\right)}{2AB.AC}=\frac{OA^2}{AB.AC}>0\)
\(\Rightarrow A\) là góc nhọn
Tương tự ta có: \(cosB=\frac{OB^2}{AB.BC}>0\) ; \(cosC=\frac{OC^2}{AC.BC}>0\) nên B, C đều nhọn
Vậy ABC là tam giác nhọn

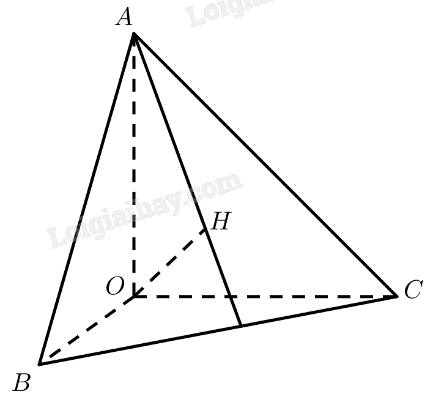
\(\begin{array}{l}\left. \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OA \bot \left( {OBC} \right) \Rightarrow OA \bot BC\\OH \bot \left( {ABC} \right) \Rightarrow OH \bot BC\\ \Rightarrow BC \bot \left( {OAH} \right) \Rightarrow BC \bot AH\end{array}\)