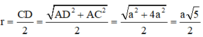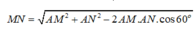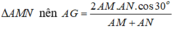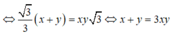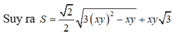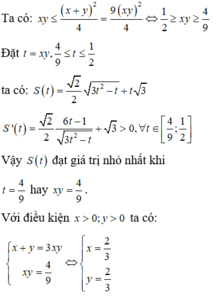Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
Kẻ hình chữ nhật \(ABCH\)
Dễ dàng tính được các độ dài: \(BD=\sqrt{10}a;BC=\sqrt{3}a,DC=\sqrt{7}a\)
\(\Rightarrow DC\perp BC\)
Ta có \(\left\{\begin{matrix} AH\perp AB\\ DA\perp AB\end{matrix}\right.\Rightarrow AB\perp (ADH)\rightarrow AB\perp DH\)
Tương tự do \(DC\perp BC,BC\perp HC\) nên \(DH\perp BC\)
\(\Rightarrow DH\perp (ABCH)\)
Theo hệ thức Pitago: \(DH=\sqrt{AD^2-AH^2}=\sqrt{6}a\)
Do đó thể tích \(ABCD\) là : \(V=\frac{S_{ABC}.DH}{3}=\frac{AB.BC.DH}{6}=\frac{\sqrt{2}a^3}{2}\)

đây là toán lớp 12 à ./ sao dễ thế bây h tui mới biết kiến thức của mình lớp 12 cớ đấy ( nói zui thui)
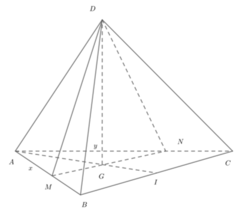
câu 2
từ A hạ đường trung tuyến \(AM\perp BC\)( tam giác ABC zuông cân tại A)
từ B hạ\(BM\perp BC\)( tam giác B'BC cân tại B (gt)
=> M là hình chiếu của B' ( ABC)
=> B'M là đường cao
xét tam giác zuông MB'A zuông tại M
=>\(B'M^2+MA^2=AB'^2\Rightarrow B'M=\sqrt{AB'^2-MA^2}\)
ta lại có
\(\frac{1}{MA^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=>\frac{1}{MA^2}=\frac{1}{a^2}+\frac{1}{a^2}=>MA=\frac{a}{\sqrt{2}}\)
=> \(B'M=\sqrt{\left(2a\right)^2-\left(\frac{a}{\sqrt{2}}\right)^2}=\frac{a\sqrt{14}}{2}\)

Phương pháp
Sử dụng công thức tính nhanh thể tích khối tứ diện biết ba cạnh và ba góc cùng xuất phát từ một đỉnh:
![]()
Cách giải:
Áp dụng công thức ![]()
ta được:
![]()
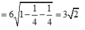
Chọn D.

Đáp án A
Chọn hệ trục tọa độ Oxy
![]()
A D = 2 a tan 60 o = 2 a 3
Từ M kẻ MH song song với AC ta có MH =a
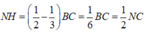
![]()
PT của mặt phẳng (BCD) là x 2 a + y 2 a + z 2 3 a = 1
Vậy khoảng cách từ
P
(
0
;
4
a
;
0
)
đến (BCD) là:
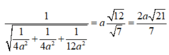

Đáp án D
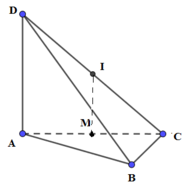
Phương pháp:
+) Xác định tâm mặt cầu ngoại tiếp khối tứ diện là điểm cách đều tất cả các đỉnh của tứ diện.
+) Áp dụng định lí Pytago tính bán kính mặt cầu ngoại tiếp tứ diện.
Cách giải:
Tam giác ABC vuông tại B, M là trung điểm của AC ⇒ M là tâm đường tròn ngoại tiếp tam giác ABC
Gọi I là trung điểm của CD ⇒ IC = ID(1)
Ta có: IM là đường trung bình của tam giác ACD ⇒ IM // AD
Mà AD ⊥ (ABC) ⇒ IM ⊥ (ABC)
Do đó, IM là trục đường tròn ngoại tiếp tam giác ABC
⇒ IA = IB = IC(2)
Từ (1), (2) ⇒ IA = IB = IC = ID ⇒ I là tâm mặt cầu ngoại tiếp tứ diện ABCD, bán kính mặt cầu: