
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



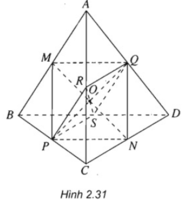
Trong tam giác ABC ta có:
MP // AC và MP = AC/2.
Trong tam giác ACD ta có:
QN // AC và QN = AC/2.
Từ đó suy ra {MP // QN}
⇒ Tứ giác MNPQ là hình bình hành.
Do vậy hai đường chéo MN và PQ cắt nhau tại trung điểm O của mỗi đường.
Tương tự: PR // QS và PR = QS = AB/2. Do đó tứ giác PQRS là hình bình hành.
Suy ra hai đường chéo RS và PQ cắt nhau tại trung điểm O của PQ và OR = OS
Vậy ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.

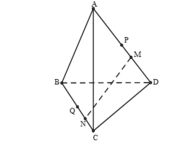
+) Do AM = 3MD; BN = 3NC suy ra:
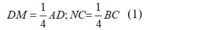
+) Do P và Q lần lượt là trung điểm của AD và BC nên :
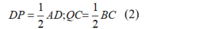
- Từ (1) và (2) suy ra: 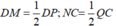
- Suy ra: M là trung điểm của DP; N là trung điểm CQ.
+) Ta có:


Chọn D.
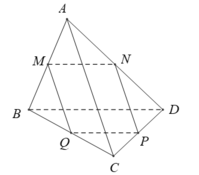
- Vì MN, PQ lần lượt là đường trung bình tam giác ABD, BCD nên:
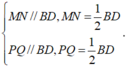
- Nên MN // PQ, MN = PQ.
⇒ tứ giác MNPQ là hình bình hành.
- Do đó MP và NQ cùng thuộc mặt phẳng MNPQ và hai đường thẳng này cắt nhau.

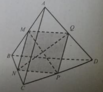
Gọi Q là trung điểm AD chứng mình MNPQ là hình bình hành ⇒ M, N, P, Q cùng thuộc một mặt phẳng ⇒ thiết diện là hình bình hành.

Ta có:
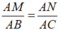
suy ra MN // BC (1) (Định lý Ta-lét đảo).
- Lại có: MN ∩ (MNI) (2)
- Từ (1) và (2) suy ra: BC // (MNI)