Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tham khảo:

Gọi I là trung điểm của BD.
Tam giác BCD có IM là đường trung bình nên IM//DC và IM=\(\dfrac{1}{2}\)CD=\(\dfrac{1}{2}\).2a=1
Tam giác ABD có IN là đường trung bình nên IN//AB và IN=\(\dfrac{1}{2}\)AB=\(\dfrac{1}{2}\).2a=1
Ta có: cos\(\widehat{MIN}\)=\(\dfrac{a^2+a^2-\left(a\sqrt{3}\right)^2}{2.a.a}=\dfrac{-1}{2}\)
Nên \(\widehat{MIN}\)=\(120^0\)
Do AB//IN, CD//IM nên góc giữa AB và CD là góc giữa IM và IN là bằng \(120^0\)

Đáp án C
Qua M vẽ đường thẳng song song với AB cắt AC tại P và vẽ đường thẳng song song với CD cắt BD tại Q. Ta có mp (MNPQ) song song với cả AB và CD. Từ đó
![]()
Áp dụng tính chất đường trung bình trong tam giác (do M, N là các trung điểm) ta suy ra được MP = MQ = NP = a hay tứ giác MPNQ là hình thoi.
Tính được
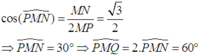

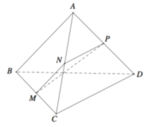
Gọi H là hình chiếu vuông góc của A lên (BCD)
\(AB=AC=AD\Rightarrow HA=HB=HC\Rightarrow H\) là tâm đáy
\(\Rightarrow DH\perp BC\)
Mà \(AH\perp\left(BCD\right)\Rightarrow AH\perp BC\)
\(\Rightarrow BC\perp\left(ADH\right)\Rightarrow BC\perp AD\)
b/ Chắc bạn nhầm đề?
Hoàn toàn tương tự câu a, ta chứng minh được \(CD\perp\left(ABH\right)\Rightarrow CD\perp AB\Rightarrow\left(AB;CD\right)=90^0\)
Điểm I để làm gì nhỉ? :<


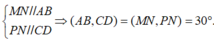
Vậy thì áp dụng định lý hàm cos:
\(cos\widehat{MIN}=\frac{IM^2+IN^2-MN^2}{2IM.IN}=\frac{a^2+2a^2-5a^2}{2.a.a\sqrt{2}}=-\frac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{MIN}=135^0\Rightarrow\) góc giữa AB và CD là \(180^0-135^0=45^0\)
Trùm Trường
IM là đường trung bình tam giác ABC \(\Rightarrow\left\{{}\begin{matrix}IM=\frac{AB}{2}=a\\IM//AB\end{matrix}\right.\)
IN là đường trung bình tam giác ACD \(\Rightarrow\left\{{}\begin{matrix}IN=\frac{CD}{2}=a\sqrt{2}\\IN//CD\end{matrix}\right.\)
\(\Rightarrow\) Góc giữa AB và CD bằng góc nhọn giữa IN và IM
Đến đây thì nhận ra là đề thiếu dữ kiện để tính, chỉ có chừng này dữ kiện ko thể tính được góc giữa 2 đường thẳng AB và CD. Chắc bạn ghi thiếu đề