Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

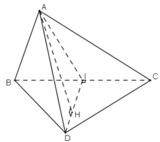
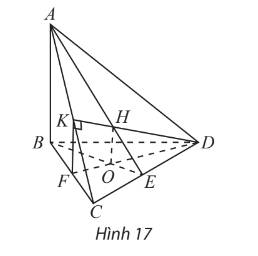
a) Tam giác ABC cân tại A có AI là đường trung tuyến nên đồng thời là đường cao:
AI ⊥ BC
+) Tương tự, tam giác BCD cân tại D có DI là đường trung tuyến nên đồng thời là đường cao:
DI ⊥ BC
+) Ta có: 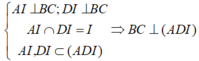
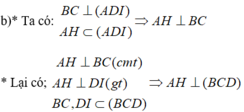

\(\left\{{}\begin{matrix}\left(ABD\right)\perp\left(BCD\right)\\\left(ABC\right)\perp\left(BCD\right)\\\left(ABC\right)\cap\left(ABD\right)=AB\end{matrix}\right.\) \(\Rightarrow AB\perp\left(BCD\right)\)
b/ \(AB\perp\left(BCD\right)\Rightarrow AB\perp CD\)
Mà \(BE\perp CD\Rightarrow CD\perp\left(ABE\right)\)
\(CD\in\left(ACD\right)\Rightarrow\left(ACD\right)\perp\left(ABE\right)\)
*/ \(\left\{{}\begin{matrix}AB\perp\left(BCD\right)\Rightarrow AB\perp DF\\DF\perp BC\end{matrix}\right.\) \(\Rightarrow DF\perp\left(ABC\right)\Rightarrow DF\perp AC\)
Mà \(DK\perp AC\Rightarrow AC\perp\left(DFK\right)\)
\(AC\in\left(ACD\right)\Rightarrow\left(ACD\right)\perp\left(DFK\right)\)

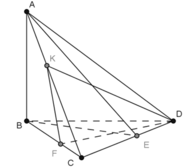
a) Ta có:
\(\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot C{\rm{D}}\\BE \bot CE\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABE} \right)\)
Lại có \(C{\rm{D}} \subset \left( {A{\rm{D}}C} \right)\)
Vậy \(\left( {ADC} \right) \bot \left( {ABE} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot DF\\DF \bot BC\end{array} \right\} \Rightarrow DF \bot \left( {ABC} \right)\\\left. \begin{array}{l} \Rightarrow DF \bot AC\\DK \bot AC\end{array} \right\} \Rightarrow AC \bot \left( {DFK} \right)\end{array}\)
Lại có \(AC \subset \left( {A{\rm{D}}C} \right)\)
Vậy \(\left( {ADC} \right) \bot \left( {DFK} \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left( {ADC} \right) \bot \left( {ABE} \right)\\\left( {ADC} \right) \bot \left( {DFK} \right)\\\left( {ABE} \right) \cap \left( {DFK} \right) = OH\end{array} \right\} \Rightarrow OH \bot \left( {ADC} \right)\)

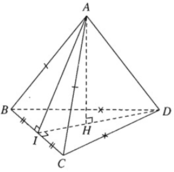
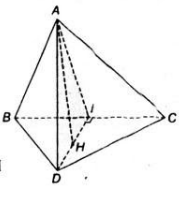
a) Tam giác ABC cân đỉnh A và có I là trung điểm của BC nên AI ⊥ BC. Tương tự tam giác DBC cân đỉnh D và có có I là trung điểm của BC nên DI ⊥ BC. Ta suy ra:
BC ⊥ (AID) nên BC ⊥ AD.
b) Vì BC ⊥ (AID) nên BC ⊥ AH
Mặt khác AH ⊥ ID nên ta suy ra AH vuông góc với mặt phẳng (BCD).

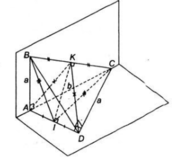


Chứng minh tương tự, ta có tam giác AKD là tam giác cân tại K có KI là đường trung tuyến nên đồng thời là đường cao.
⇒ IK ⊥ AD (2)
Từ (1) và (2) suy ra; IK là đường vuông góc chung của hai đường thẳng AD và BC.
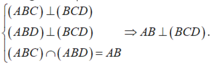
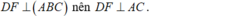
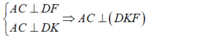
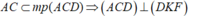
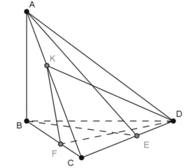
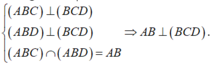
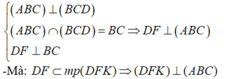
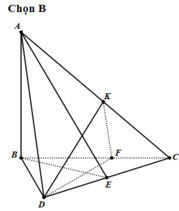
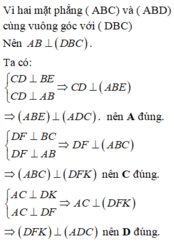

- Theo giả thiết:
Ta có:
- Lại có: