Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác ABC.Vẽ về phía ngoài tam giác các hình vuông ABDE và ACFG có tâm theo thứ tự là M,N.Gọi I,K theo thứ tự là trung điểm của EG,BC. - Hình học - Diễn đàn Toán học

a: Kẻ CH vuông góc với AM
\(S_{AGC}=\dfrac{CH\cdot AG}{2}\)
\(S_{GMC}=\dfrac{CH\cdot MG}{2}\)
mà AG=2MG
nên \(S_{AGC}=2S_{GMC}\)
b: Kẻ GK vuông góc với BC
\(S_{GMB}=\dfrac{BM\cdot GK}{2}\)
\(S_{GMC}=\dfrac{MC\cdot GK}{2}\)
mà BM=CM
nên \(S_{GMB}=S_{GMC}\)

Bài 2:
Ta có: AM=1/2BC
nên AM=BM=CM
Xét ΔMAB có MA=MB
nên ΔMAB cân tại M
=>\(\widehat{MAB}=\widehat{B}\)
Xét ΔMAC có MA=MC
nên ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{C}\)
Xét ΔBAC có \(\widehat{BAC}+\widehat{B}+\widehat{C}=180^0\)
\(\Leftrightarrow\widehat{MAB}+\widehat{B}+\widehat{MAC}+\widehat{C}=180^0\)
\(\Leftrightarrow2\cdot\left(\widehat{MAB}+\widehat{MAC}\right)=180^0\)
=>\(\widehat{BAC}=90^0\)
hay ΔABC vuông tại A

Lập luận tương tự câu c), ta có BF là một đường cao của tam giác LBC.
Vậy ba đường thẳng AH, BF, CD là ba đường cao của tam giác LBC nên chúng đồng quy.

Xét tam giác ALB và ∆BCD có:
AL = BC ( chứng minh b)
AB = BD ( vì ABDE là hình vuông)
∠(BAL) = 90º + ∠(EAL) = 90 + ∠(ABC) = ∠(DBC) .
Suy ra: ∆ALB = ∆BCD ( c.g.c)
Suy ra ∠(ALB) = ∠(BCD) .
Mặt khác ta có ∠(ALB) + ∠(LBH) = 90º nên ∠(BCD) + ∠(LBH) = 90º.
Suy ra LB ⊥ CD, tức CD là một đường cao của tam giác LBC.

Theo a) ΔEKI = ΔGKJ nên KI = KJ.
Mặt khác, theo giả thiết K là trung điểm của AL nên KA = KL.
Suy ra: KA – KI = KL – KJ hay IA= JL.
Ta có: ∆ACH= ∆ GAJ ( theo a) nên HC = AJ;
∆ABH = ∆ EAI nên BH = AI.
+) Suy ra:
AL = AJ + JL = AJ + AI = HC + HB = BC

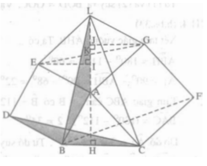
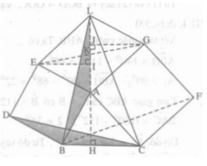
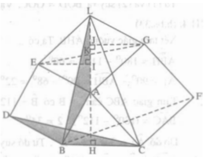
Ta có : AC//DB\(\Rightarrow S_{ABD}=S_{CDB}\left(1\right)\)
\(\Delta CDB=\Delta KAB\Rightarrow S_{CDB}=S_{KAB}\left(2\right)\)
AI//BK\(\Rightarrow S_{KAB}=S_{KIB}\left(3\right)\)
Từ (1),(2) và (3) suy ra \(S_{ABD}=S_{KIB}\Leftrightarrow S_{ABDE}=S_{BIJK}\left(4\right)\)
Với I,J là hình chiếu A xuống BC,HK
Tương tự ta cx có \(S_{ACFG}=S_{IJHC}\left(5\right)\)
Cộng (4) vfa (5) có ĐPCM
Từ đó suy ra Đ.L.Pitago
kì tích nhỉ ( 1 ) CM hơi bị kì tích