Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
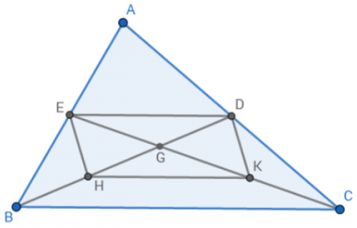
BD là đường trung tuyến của Δ ABC nên D là trung điểm của AC (1)
CE là đường trung tuyến của Δ ABC nên E là trung điểm của AB (2)
Từ (1) và (2) suy ra :
DE là đường trung bình của Δ ABC
=> DE // BC và DE = 1/2 BC
Δ BGC có H là trung điểm của GB và K là trung điểm của GC
suy ra HK là đường trung bình của Δ BGC
=> HK // BC và HK = 1/2 BC
Tứ giác DEHK có DE//BC, HK // BC và DE = HK = 1/2 BC
nên tứ giác
b) DEHK là hình bình hành nên
HG = GD = 1/2 HD và GE = GK = 1/2 EK
Để tứ giác DEHK là hình chữ nhật thì
HD = EK => 1/2 HD = 1/2 EK => GE = GD và GH = GK
GH = GK => 2GH = 2GK => GB = GC
Xét Δ GEB và Δ GDC có
GE = GD Góc EGB = góc DGC GB = GC => ΔGEB = ΔGDC (c.g.c) => BE = CD => 2BE = 2CD => AB = AC => ΔABC cân tại A Vậy đểtứ giác DEHK là hình chữ nhật thì
ΔABC cân tại Ac) BD ⊥ CE => HD ⊥ EK Hình bình hành DEHK có HD ⊥ EK nên DEHK là hình thoi Vậy
nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình thoi

Sửa đề: Đường trung tuyến BD
a) Ta có: BD và CE lần lượt là các đường trung tuyến ứng với các cạnh AC,AB trong ΔABC(gt)
nên E là trung điểm của AB và D là trung điểm của AC
Xét ΔABC có
E là trung điểm của AB(cmt)
D là trung điểm của AC(cmt)
Do đó: ED là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: ED//BC và \(ED=\dfrac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)(1)
Xét ΔGBC có
H là trung điểm của GB(gt)
K là trung điểm của GC(gt)
Do đó: HK là đường trung bình của ΔGBC(Định nghĩa đường trung bình của tam giác)
Suy ra: HK//BC và \(HK=\dfrac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra ED//HK và ED=HKXét tứ giác EDKH có
ED//HK(cmt)
ED=HK(cmt)
Do đó: EDKH là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Sửa đề: Đường trung tuyến BD
a) Ta có: BD và CE lần lượt là các đường trung tuyến ứng với các cạnh AC,AB trong ΔABC(gt)
nên E là trung điểm của AB và D là trung điểm của AC
Xét ΔABC có
E là trung điểm của AB(cmt)
D là trung điểm của AC(cmt)
Do đó: ED là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: ED//BC và ED=BC2ED=BC2(Định lí 2 về đường trung bình của tam giác)(1)
Xét ΔGBC có
H là trung điểm của GB(gt)
K là trung điểm của GC(gt)
Do đó: HK là đường trung bình của ΔGBC(Định nghĩa đường trung bình của tam giác)
Suy ra: HK//BC và HK=BC2HK=BC2(Định lí 2 về đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra ED//HK và ED=HKXét tứ giác EDKH có
ED//HK(cmt)
ED=HK(cmt)
Do đó: EDKH là hình bình hành(Dấu hiệu nhận biết hình bình hành)

A B C E D H K G
a) Ta có:
DE là đường trung bình của tam giác ABC =>DE//= \(\frac{1}{2}\)BC
HK là đường trung bình của tam giác GBC => HK //=\(\frac{1}{2}\)BC (1)
=> DE//=HK => DEHK là hình bình hành
b) DEHK là hình chữ nhật
điều kiện là: HE vuông góc HK
mà HE là đường trung bình tam giác ABG => HE//=\(\frac{1}{2}\)AG
lại có: HK //=\(\frac{1}{2}\)BC ( theo (1))
=> AG vuông góc BC => AG là đường cao của tam giác ABC (2)
mà hai đường trung tuyến BD và CE cắt nhau tại G => G là trọng tâm tam giác ABC => AG là đường trung tuyến ABC (3)
Từ (2), (3) => tam giác ABC cân
c) Khi BD vuông góc với CE
=> hình chữ nhật EDKH có EK vuông HD
=> EDKH là hình vuông.

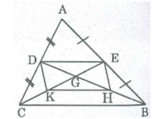
Hình bình hành DEHK trở thành hình chữ nhật khi DH = EK
Mà DH = 2/3 BD; EK = 2/3 CE
Nên DH = EK ⇒ BD = CE
⇒ ∆ ABC cân tại A.
Vậy ∆ ABC cân tại A thì tứ giác DEHK là hình chữ nhật.


A B C D E G H K M
a) Xét \(\Delta ABC\)có:
\(AE=BE\)(giả thiết)
\(AD=CD\)(giả thiết)
\(\Rightarrow DE\)là đường trung bình của \(\Delta ABC\)
\(\Rightarrow DE//BC\)(tính chất) (1)
Và \(2DE=BC\)(tính chất) (2)
Xét \(\Delta GBC\)có:
\(GH=BH\)(giả thiết)
\(GK=CK\)(giả thiết)
\(\Rightarrow HK\)là đường trung bình của \(\Delta ABC\)
\(\Rightarrow HK//BC\)(tính chất) (3)
Và \(2HK=BC\)(tính chất) (4)
Từ (1) và (3)
\(\Rightarrow ED//HK\)(5)
Từ (2) và (4)
\(\Rightarrow2DE=2KH\Rightarrow DE=KH\)(6)
Xét tứ giác DEHK có: (5) và (6).
\(\Rightarrow DEHK\)là hình bình hành (điều phải chứng minh)