Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Gọi số có 4 chữ số thỏa mãn đề là $\overline{a_1a_2a_3a_4}$
$a_1=0, 1$ (do $a_1a_2a_3a_4}<2000$) => $a_1$ có 2 cách chọn.
$a_2$ có 9 cách chọn (0,1, 3,4,5,6,7,8,9)
$a_3$ có 9 cách chọn (0,1,3,4,5,6,7,8,9)
$a_4$ có 9 cách chọn (0,1,3,4,5,6,7,8,9)
Vậy có $2.9.9.9=1458$ số tự nhiên thỏa đề.

Tập A có n phần tử:
Số tập con có 3 phân tử là: \(C_n^3=\frac{n!}{3!\left(n-3\right)!}=\frac{n\left(n-1\right)\left(n-2\right)}{6}\)
Số tập con 2 phần tử là : \(C_n^2=\frac{n!}{2!\left(n-2\right)!}=\frac{n\left(n-1\right)}{2}\)
Theo bài ra ta có: \(\frac{n\left(n-1\right)\left(n-2\right)}{6}-\frac{n\left(n-1\right)}{2}=14\)<=> \(n^3-6n^2+5n-84=0\Leftrightarrow n=7\)
Vậy tập A có 7 phần tử

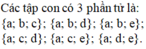

a. Các tập thỏa mãn là tập con chứa số 2 của \(\left\{2;3;4;5;6;7\right\}\)
Số tập này bằng số tập con của \(B=\left\{3;4;5;6;7\right\}\) là tập có 5 phần tử (tìm các tập con của B, sau đó với mỗi tập con tìm được ta thêm số 2 vào là được)
\(\Rightarrow\) Có \(2^5=32\) tập thỏa mãn
(Câu a chỉ cần trình bày thế này, bỏ 2 chỗ ngoặc đơn đi là được)
b.
Tương tự, ta chỉ cần tìm tập con có 1 phần tử của \(\left\{3;4;5;6;7\right\}\)
\(\Rightarrow\) Có 5 tập thỏa mãn
Câu b có thể trình bày bằng cách liệt kê:
Các tập hợp thỏa mãn là: \(\left\{1;3\right\};\left\{1;4\right\};\left\{1;5\right\};\left\{1;6\right\};\left\{1;7\right\}\) có 5 tập thỏa mãn
(câu a có tới 32 tập nên chỉ cần biện luận, không nên liệt kê ra)
Nếu như mình trình bày bài làm thì ghi sao cho đúng ạ ?