Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

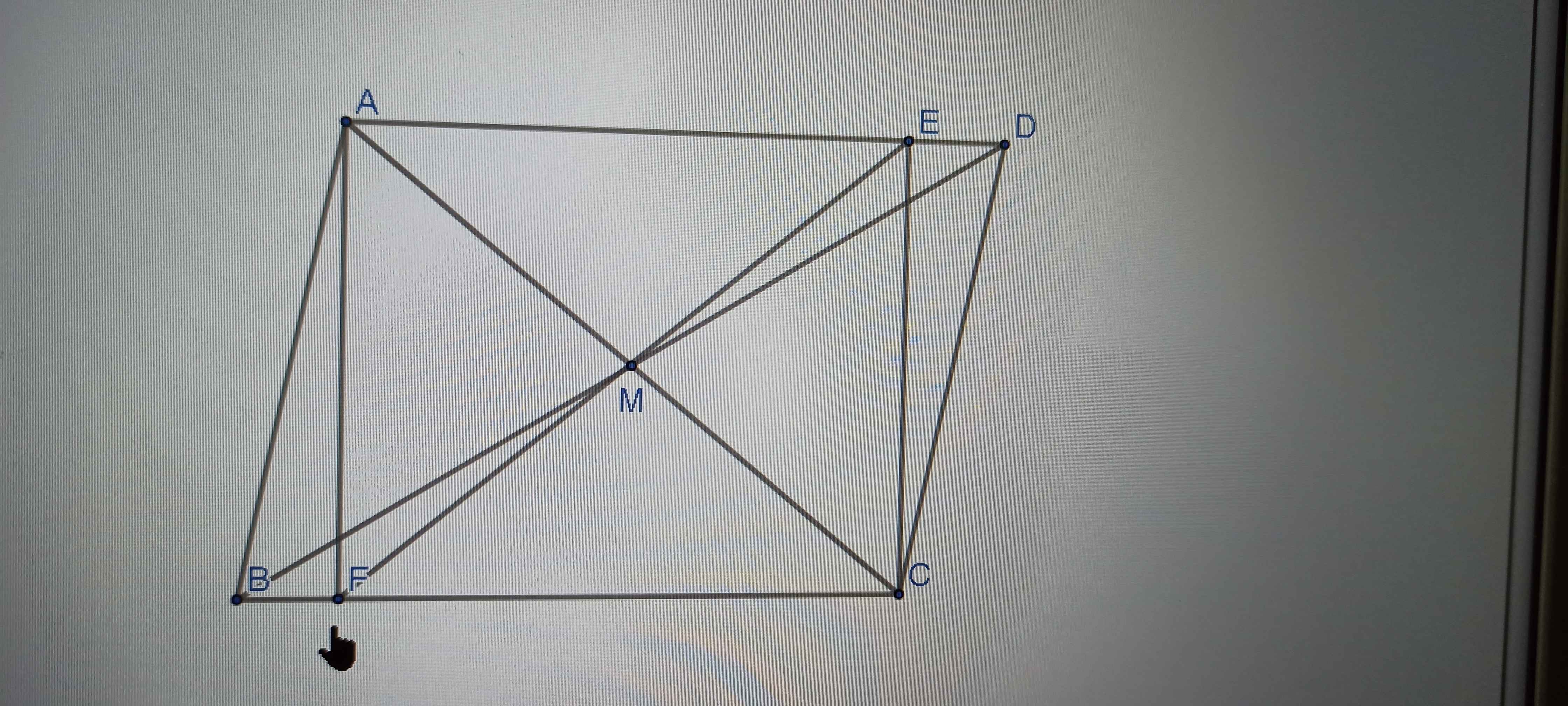
 a) Xét ∆ABM và ∆CDM có:
a) Xét ∆ABM và ∆CDM có:
AM = CM (gt)
AMB = CMD (đối đỉnh)
BM = DM (gt)
⇒ ∆ABM = ∆CDM (c-g-c)
b) Do ∆ABM = ∆CDM (cmt)
⇒ MAB = MCD (hai góc tương ứng)
⇒ MCD = 90⁰
⇒ MC ⊥ CD
⇒ AC ⊥ CD

Câu C bạn cm AFCE là hình chữ nhật , FE là đường chéo => E,F,M thẳng hàng vì 2 đường chéo hình chữ nhật đi qua trung điểm của mỗi đường.

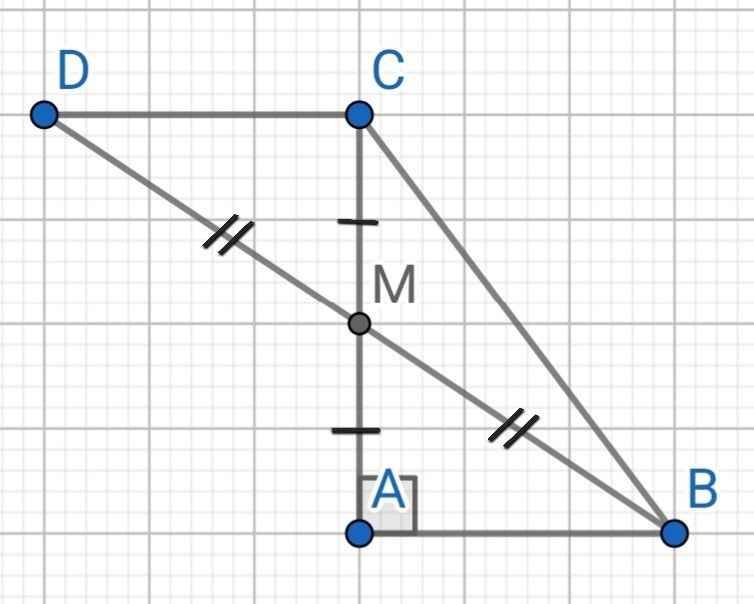
a: AC=căn 5^2-3^2=4cm
b: Xét ΔMAB và ΔMCD có
MA=MC
góc AMB=góc CMD
MB=MD
=>ΔMAB=ΔMCD
=>AB=CD
c: AB+BC=CD+BC>DB=2BM(ĐPCM)

A) Vì tam giác ABC vuông tại A nên ta có :
AB2+AC2=BC2AB2+AC2=BC2
⇔AC2=BC2−AB2⇔AC2=BC2−AB2
⇔AC2=52−32⇔AC2=52−32
⇔AC2=25−9⇔AC2=25−9
⇔AC2=16⇔AC2=16
⇔AC=4

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Xét ΔMBA và ΔMCD có
MB=MC
\(\widehat{AMB}=\widehat{DMC}\)
MA=MD
Do đó: ΔMBA=ΔMCD

a) Xét ΔABM và ΔCDM có
MA=MC(M là trung điểm của AC)
\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)
MB=MD(gt)
Do đó: ΔABM=ΔCDM(c-g-c)
b) Ta có: ΔABM=ΔCDM(cmt)
nên \(\widehat{MAB}=\widehat{MCD}\)(hai góc tương ứng)
mà \(\widehat{MAB}=90^0\)(gt)
nên \(\widehat{MCD}=90^0\)
\(\Leftrightarrow\widehat{ACD}=90^0\)
hay AC\(\perp\)CD(Đpcm)

a)
Sửa đề: Chứng minh ΔMAB=ΔMCD và \(\widehat{MCD}=90^0\)
Xét ΔMAB và ΔMCD có
MA=MC(M là trung điểm của AC)
\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)
MB=MD(gt)
Do đó: ΔMAB=ΔMCD(c-g-c)
Suy ra: \(\widehat{MAB}=\widehat{MCD}\)(hai góc tương ứng)
mà \(\widehat{MAB}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{MCD}=90^0\)(đpcm)
b) Xét ΔDMA và ΔBMC có
DM=BM(gt)
\(\widehat{DMA}=\widehat{BMC}\)(hai góc đối đỉnh)
MA=MC(M là trung điểm của AC)
Do đó: ΔDMA=ΔBMC(c-g-c)
Suy ra: \(\widehat{ADM}=\widehat{CBM}\)(hai góc tương ứng)
mà \(\widehat{ADM}\) và \(\widehat{CBM}\) là hai góc ở vị trí so le trong
nên AD//BC(Dấu hiệu nhận biết hai đường thẳng song song)
c)
Ta có: MB=MD(gt)
mà D,M,B thẳng hàng(gt)
nên M là trung điểm của BD
Xét ΔMAB vuông tại A và ΔMAK vuông tại A có
MA chung
AB=AK(gt)
Do đó: ΔMAB=ΔMAK(hai cạnh góc vuông)
Suy ra: MB=MK(hai cạnh tương ứng)
mà \(BD=2\cdot MB\)(M là trung điểm của BD)
nên \(BD=2\cdot MK\)(đpcm)