Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

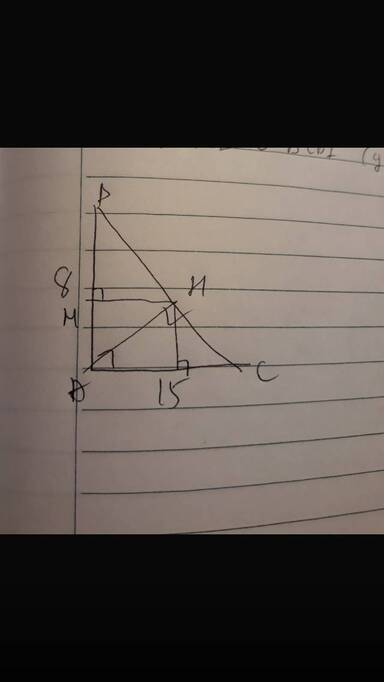
A B C 8 15 H M N 8
a, Xét tam giác ABC vuông tại A, đường cao AH
\(AB^2+AC^2=BC^2\Rightarrow BC^2=64+225=289\Rightarrow BC=17\)cm
Xét tam giác AHC và tam giác BAC ta có :
^AHC = ^BAC = 900
^C _ chung
Vậy tam giác AHC ~ tam giác BAC ( g.g )
\(\Rightarrow\frac{AH}{AB}=\frac{AC}{BC}\)( tỉ số đồng dạng )
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{8.15}{17}=\frac{120}{17}\)cm
b, Vì MH vuông AB
NA vuông AB
=> MH // NA tương tự ta có : MH // AN
=> tứ giác AMNH là hình bình hành
mà ^HNA = 900 ; ^BAC = 900 ; ^HMA = 900
=> tứ giác AMHN là hình vuông

a) XétΔABC vg tại A
⇒ BC²=AB²+AC²
⇒ BC=17cm
Xét ΔABH và ΔCBA có:
góc AHB= góc CBA
góc B: chung
⇒ ΔABH ∞ ΔCBA (g.g)
⇒ AB/BC=BH/BA
⇒ BH=AB²/BC
⇒ BH=64/17
Xét ΔABH vg tại H
⇒AB²=BH²+AH²
⇒ AH=120/17
b) xét tg AMHN có: góc AMH= góc ANH= góc MAN=90
⇒ tg AMHN là hcn (dhnb)
⇒ AH=MN (t/c hcn)
⇒ MN=120/17
, Ta thấy tam giác AMH đồng dạng tam giác AHB (g.g) suy ra AM/AH = AH/ AB => AM.AB =AH^2
tam giác ANH đồng dạng tam giác AHC (g.g)
=> AN/AH = AH/AC
=> AN.AC = AH^2
suy ra AM.AB = AN.AC.