Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

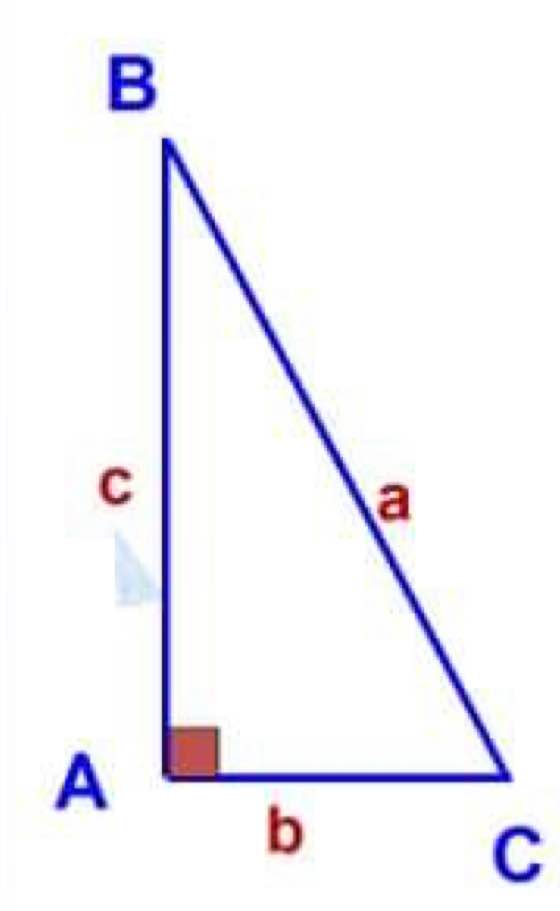
a: \(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AC}{BC}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{AB}{BC}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{AC}{AB}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{AB}{AC}\)

A B C
Sin B = \(\frac{AC}{BC}\); cos B = \(\frac{AB}{BC}\) ; tgB = \(\frac{AC}{AB}\); cot gB = \(\frac{AB}{BC}\)
Do góc B và C là hai góc phụ nhau nên :
sin C = cos B = \(\frac{AB}{BC};cosB=\frac{AB}{BC};cosC=sinB=\frac{AC}{BC}\)
\(tgC=cotgB=\frac{AB}{BC};cotgC=tgB=\frac{AC}{AB}\)
Chúc bạn học tốt !!!

Đặt cạnh BC=a=8; AB=c; AC=b
Kẻ đường cao AH. Xét tg vuông ABH có ^BAH=90-^B=90-60=30
=> BH=AB/2=c/2 (trong tg vuông cạnh đối diện góc 30 =1/2 cạnh huyền)
\(\Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{c^2-\frac{c^2}{4}}=\frac{c\sqrt{3}}{2}.\)
\(S_{ABC}=\frac{1}{2}.BC.AH=\frac{1}{2}.8.\frac{c\sqrt{3}}{2}=2c\sqrt{3}\)
Nửa chu vi p=(a+b+c)/2=(8+12)/2=10
Áp dụng công thức he rông
\(S_{ABC}=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{10\left(10-8\right)\left(10-b\right)\left(10-c\right)}\)
\(=\sqrt{20\left(100-10c-10b+bc\right)}=\sqrt{20\left(100-10\left(c+b\right)+bc\right)}\)
\(=\sqrt{20\left(100-10.12+bc\right)}=\sqrt{20\left(bc-20\right)}=2c\sqrt{3}\)
Bình phương 2 vê \(20\left(bc-20\right)=12c^2\) (*)
Thay b=12-c vào (*) rồi giải PT bậc 2 tìm c từ đó suy ra b. Bạn tự làm nốt nhé, chúc học tốt!
T