Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

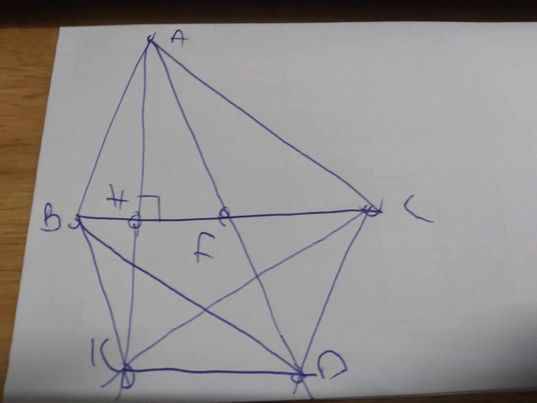
Xét tứ giác ABDC có
F là trung điểm chung của AD và BC
Do đó: ABDC là hình bình hành
=>BD=AC(1)
Xét ΔCAK có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAK cân tại C
=>CA=CK(2)
Từ (1) và (2) suy ra BD=AC=CK

F là trung điểm của AD
=>FA=FD
F là trung điểm của BC
=>FB=FC
Xét ΔFAC và ΔFDB có
FA=FD
\(\widehat{AFC}=\widehat{DFB}\)
FC=FB
Do đó: ΔFAC=ΔFDB
=>\(\widehat{FAC}=\widehat{FDB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD

F là trung điểm của AD
=>FA=FD
F là trung điểm của BC
=>FB=FC
Xét ΔFAC và ΔFDB có
FA=FD
\(\widehat{AFC}=\widehat{DFB}\)
FC=FB
Do đó: ΔFAC=ΔFDB
=>\(\widehat{FAC}=\widehat{FDB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD

F là trung điểm của AD
=>FA=FD
F là trung điểm của BC
=>FB=FC
Xét ΔFAC và ΔFDB có
FA=FD
\(\widehat{AFC}=\widehat{DFB}\)
FC=FB
Do đó: ΔFAC=ΔFDB
=>\(\widehat{FAC}=\widehat{FDB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD

F là trung điểm của BC
=>FB=FC
F là trung điểm của AD
=>AF=FD


Xét ΔABF và ΔDCF có
FA=FD
\(\widehat{AFB}=\widehat{DFC}\)
FB=FC
Do đó: ΔABF=ΔDCF

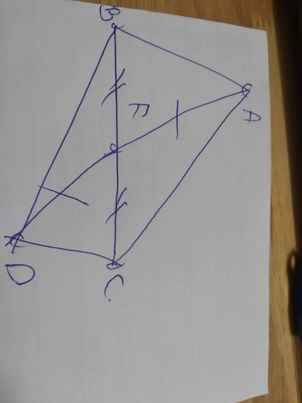
a, xét tma giác AEB và tam giác DEC có :
BE = EC do E là trđ của BC (Gt)
AE = ED do E là trđ của AD (gt)
góc BEA = góc DEC (đối đỉnh)
=> tam giác AEB = tam giác DEC (c-g-c)
b, xét tam giác CEA và tam giác BED có:
BE = EC (Câu a)
AE = ED (câu a)
góc BED = góc CEA (đối đỉnh)
=> tam giác CEA = tam giác BED (c-g-c)
=> góc DBE = góc ECA (đn) mà 2 góc này slt
=> CA // BD (Đl)
c, xét tam giác AHC và tam giác KHC có : HC chung
AH = HK do K là trđ của AH (gt)
góc AHC = góc KHC =90
=> tam giác AHC = tam giác KHC (2cgv)
=> AC = CK (đn)
mà AC = BD do tam giác BED = tam giác CEA (Câu b)
=> BD = AC = CK
Xét ΔAKD có
H,F lần lượt là trung điểm của AK,AD
Do đó: HF là đường trung bình của ΔAKD
=>HF//KD
Ta có: KD//HF
\(H,F\in BC\)
Do đó: KD//BC
Ta có: KD//BC
AH\(\perp\)BC
Do đó: AH\(\perp\)DK