Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔAKD có
H,F lần lượt là trung điểm của AK,AD
Do đó: HF là đường trung bình của ΔAKD
=>HF//KD
Ta có: KD//HF
\(H,F\in BC\)
Do đó: KD//BC
Ta có: KD//BC
AH\(\perp\)BC
Do đó: AH\(\perp\)DK

F là trung điểm của AD
=>FA=FD
F là trung điểm của BC
=>FB=FC
Xét ΔFAC và ΔFDB có
FA=FD
\(\widehat{AFC}=\widehat{DFB}\)
FC=FB
Do đó: ΔFAC=ΔFDB
=>\(\widehat{FAC}=\widehat{FDB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD

F là trung điểm của AD
=>FA=FD
F là trung điểm của BC
=>FB=FC
Xét ΔFAC và ΔFDB có
FA=FD
\(\widehat{AFC}=\widehat{DFB}\)
FC=FB
Do đó: ΔFAC=ΔFDB
=>\(\widehat{FAC}=\widehat{FDB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD

F là trung điểm của AD
=>FA=FD
F là trung điểm của BC
=>FB=FC
Xét ΔFAC và ΔFDB có
FA=FD
\(\widehat{AFC}=\widehat{DFB}\)
FC=FB
Do đó: ΔFAC=ΔFDB
=>\(\widehat{FAC}=\widehat{FDB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD

F là trung điểm của BC
=>FB=FC
F là trung điểm của AD
=>AF=FD


a, xét tma giác AEB và tam giác DEC có :
BE = EC do E là trđ của BC (Gt)
AE = ED do E là trđ của AD (gt)
góc BEA = góc DEC (đối đỉnh)
=> tam giác AEB = tam giác DEC (c-g-c)
b, xét tam giác CEA và tam giác BED có:
BE = EC (Câu a)
AE = ED (câu a)
góc BED = góc CEA (đối đỉnh)
=> tam giác CEA = tam giác BED (c-g-c)
=> góc DBE = góc ECA (đn) mà 2 góc này slt
=> CA // BD (Đl)
c, xét tam giác AHC và tam giác KHC có : HC chung
AH = HK do K là trđ của AH (gt)
góc AHC = góc KHC =90
=> tam giác AHC = tam giác KHC (2cgv)
=> AC = CK (đn)
mà AC = BD do tam giác BED = tam giác CEA (Câu b)
=> BD = AC = CK

Xét ΔABF và ΔDCF có
FA=FD
\(\widehat{AFB}=\widehat{DFC}\)
FB=FC
Do đó: ΔABF=ΔDCF
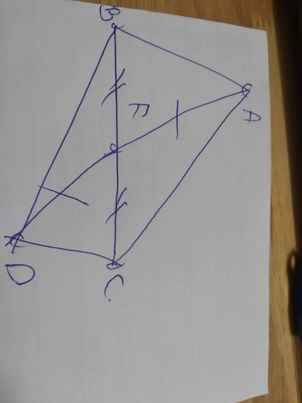
Xét tứ giác ABDC có
F là trung điểm chung của AD và BC
Do đó: ABDC là hình bình hành
=>BD=AC(1)
Xét ΔCAK có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAK cân tại C
=>CA=CK(2)
Từ (1) và (2) suy ra BD=AC=CK