Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
202 = AH2 + 162
400 = AH2 + 256
AH2 = 400 - 256
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
AC2 = 122 + 52
AC2 = 144 + 25
AC2 = 169
AC = \(\sqrt{169}\)= 13 (cm)
Vậy AH = 12 cm
AC = 13 cm
Bài 2:
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
152 = AH2 + 92
225 = AH2 + 81
AH2 = 225 - 81
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHB vuông tại, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = \(\sqrt{169}\)= 13 (cm)
Vậy AB = 13 cm

A B H C
Xét \(\Delta\)AHC vuông tại H:
=> AC2 = HA2 + HC2
HC2 = AC2 - HA2
HC2 = 202 - 122 = 256
HC = \(\sqrt{256}\) = 16 (cm)
BC = BH + HC
BC = 5 + 16 = 21 (cm)
Xét \(\Delta\)AHB vuông tại H
=> AB2 = HA2 + HB2
AB2 = 122 + 52
AB2 = 144 + 25 = 169
AB = \(\sqrt{169}\) = 13 (cm)
Chu vi của \(\Delta\)ABC là:
AC + CB + BA = 20 + 21 + 13
= 54 (cm)
Vậy chu vi của \(\Delta\)ABC là 54 cm.

Tam giác AHC vuông tại H nên :
AC2 = AH2 + HC2
202 = 122 + HC2
=> HC2 = 202 - 122
HC2 = 400 - 144 = 256 = 162
=> HC = 16 cm
Ta có : BC = HC + HB = 16 + 5 = 21 cm
Tam giác ABH vuông tại H nên :
AB2 = AH2 + HB2
AB2 = 122 + 52
AB2 = 144 + 25 = 169 = 132
=> AB = 13 cm
Vậy chu vi tam giác ABC là :
AB + AC + BC = 13 + 20 + 21 = 54 (cm)

Theo gt ta có : AH vuông góc với BC
=> \(\Delta\) AHB và \(\Delta\) AHC là \(\Delta\) vuông
Xét : \(\Delta\) AHB có : AH\(^2\)+ HB\(^2\) = AB\(^2\)
mà : AH = 12cm, HB = 5cm
=> AB\(^2\)= 12\(^2\)+ 5\(^2\)
=> AB\(^2\)= 144 + 25
=> AB\(^2\)= 169
=> AB = 13 cm (1)
Tương tự ta cũng có :
=> AC\(^2\)= 12\(^2\)+ 16\(^2\)
=> AB\(^2\)= 144 + 256
=> AB\(^2\)= 400
=> AB = 20 cm (2)
Mặt khác : BC = BH + CH
=> BC = 5 + 16 = 21cm (3)
Từ : (1), (2), (3) => chu vi tam giác ABC = 13 + 20 + 21 = 54 cm

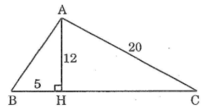
∆AHB có ∠(AHB) =90°
Theo định lý pitago, ta có:
AB2=AH2+HB2
= 122+52=169
Vậy AB = 13 cm
∆AHC có ∠(AHC) =90o
Theo định lý pitago, ta có:
AC2=AH2+HC2
HC2=AC2-AH2=202-122=400-144=256
Vậy HC = 16cm
Ta có: BC = BH + HC = 5 +16 = 21cm
Chu vi tam giác ABC là: AB + AC + BC = 13 + 20 + 21 = 54cm

tam giác AHB vuông tại H ,THEO ĐỊNH LÝ PYTA GO TA CÓ
AB^2=AH^2+BH^2=>AB^2=169=>AB=13 CM
TAM GIÁC AHC VUÔNG TẠI H,THEO ĐỊNH LÝ PYTA GO TA CÓ
HC^2+AH^2=AC^2=>HC^2=AC^2-AH^2=>HC^2=256=>HC=16CM
VÌ H NẰM GIỮA BC => BC=BH+HC=21 CM
=>CHU VI TAM GIÁC ABC LÀ
AB+AC+BC=13+21+20=54 CM

chỉ giúp em giải toán với