Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b: góc DFC=góc EBC
góc EFC=góc DAC
góc EBC=góc DAC
=>góc DFC=góc EFC

a) Do BE và CF là các đường cao trong tam giác ABC nên ˆBEC=90∘, ˆBFC=90∘
Tứ giác BCEF có góc E và góc F cùng nhìn cạnh BC và bằng nhau (cùng bằng 90∘) nên là tứ giác nội tiếp.
b) Tứ giác BCEF là tứ giác nội tiếp nên ˆAFE=ˆACB, mà ˆACB=ˆASB (cùng chắn cung AB) nên ˆAFE=ˆASB
Suy ra tứ giác BFMS là tứ giác nội tiếp.
Do đó ˆFMS=180∘−ˆFBS=90∘.. Vậy OA ⊥⊥ EF.
c)
+) Tứ giác BCEF nội tiếp nên ˆAEF=ˆABC (1)
Từ OA ⊥ PE suy ra ˆAIB=ˆAPE(cùng phụ với ˆMAP). (2)
Từ (1) và (2) suy ra ΔAPE∽ΔABI (g.g).
+) Tứ giác BHCS có BH // CS (cùng vuông góc với AS) và BS // CH (cùng vuông góc với AB) nên là hình bình hành. Do đó ba điểm H, K, S thẳng hàng.
Ta sẽ chứng minh hai góc đồng vị ˆPIM và HSM^ bằng nhau.
Tứ giác PDIM nội tiếp (vì có hai góc vuông M và D đối nhau) nên ˆPIM=ˆPDM (3)
Ta có:
ΔAHE∽ΔACDΔ nên AH.AD = AE.AC.
ΔAME∽ΔACSnên AM.AS = AE.AC.
Suy ra AH.AD = AM.AS ⇒AH/AM=AS/AD.
Do đó ΔMAH∽ΔDAS(c.g.c). Suy ra AHM^=ASD^.
Từ đó ta có tứ giác DHMS là tứ giác nội tiếp. Suy ra ˆHDM=ˆHSM. (4)
Từ (3) và (4) suy ra HS // PI, hay KH // PI.

\({}\)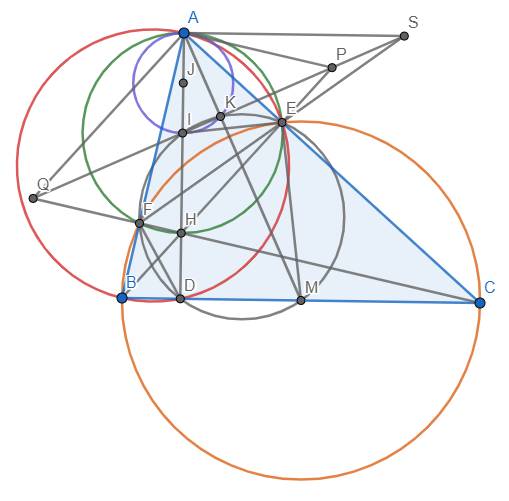
a) Vì \(\widehat{BEC}=\widehat{BFC}=90^o\) nên tứ giác BEFC nội tiếp đường tròn đường kính BC. Tương tự như thế, tứ giác AEDB nội tiếp đường tròn đường kính AB. Cũng có \(\widehat{AEH}=\widehat{AFH}=90^o\) nên tứ giác AEHF nội tiếp đường tròn đường kính AH.
Ta có \(\widehat{IEM}=\widehat{IEB}+\widehat{BEM}\)
\(=\left(90^o-\widehat{IEA}\right)+\widehat{EBC}\)
\(=90^o-\widehat{EAD}+\widehat{EBD}=90^o\) (do \(\widehat{EBD}=\widehat{EAD}\))
Vậy \(IE\perp ME\)
b) Dễ thấy các điểm I, D, E, F, M, K cùng thuộc đường tròn đường kính IM. Gọi J là trung điểm AI thì I chính là tâm của đường tròn (AIK) nên (J) tiếp xúc với (I) tại A. Dẫn đến A nằm trên trục đẳng phương của (I) và (J)
Mặt khác, ta có \(SK.SI=SE.SF\) nên \(P_{S/\left(I\right)}=P_{S/\left(J\right)}\) hay S nằm trên trục đẳng phương của (I) và (J). Suy ra AS là trục đẳng phương của (I) và (J). \(\Rightarrow\)\(AS\perp IJ\) hay AS//BC (đpcm).
c) Ta thấy tứ giác AKEP nội tiếp đường tròn AP
\(\Rightarrow\widehat{APB}=\widehat{MKE}=\widehat{MDE}=\widehat{BAC}\)
\(\Rightarrow\Delta BAE~\Delta BPA\left(g.g\right)\Rightarrow\widehat{BAP}=\widehat{BEA}=90^o\)
\(\Rightarrow\) AP//QH \(\left(\perp AB\right)\)
\(\Rightarrow\widehat{IAP}=\widehat{IHQ}\) (2 góc so le trong)
Từ đó dễ dàng chứng minh \(\Delta IAP=\Delta IHQ\left(g.c.g\right)\) \(\Rightarrow IP=IQ\) hay I là trung điểm PQ (đpcm)