Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔMNE vuông tại E và ΔKNE vuông tại E có
NE chung
góc MNE=góc KNE
=>ΔMNE=ΔKNE
b: Xét ΔNMD và ΔNKD có
NM=NK
góc MND=góc KND
ND chung
=>ΔNMD=ΔNKD
=>góc NKD=90 độ
=>DK vuông góc NP

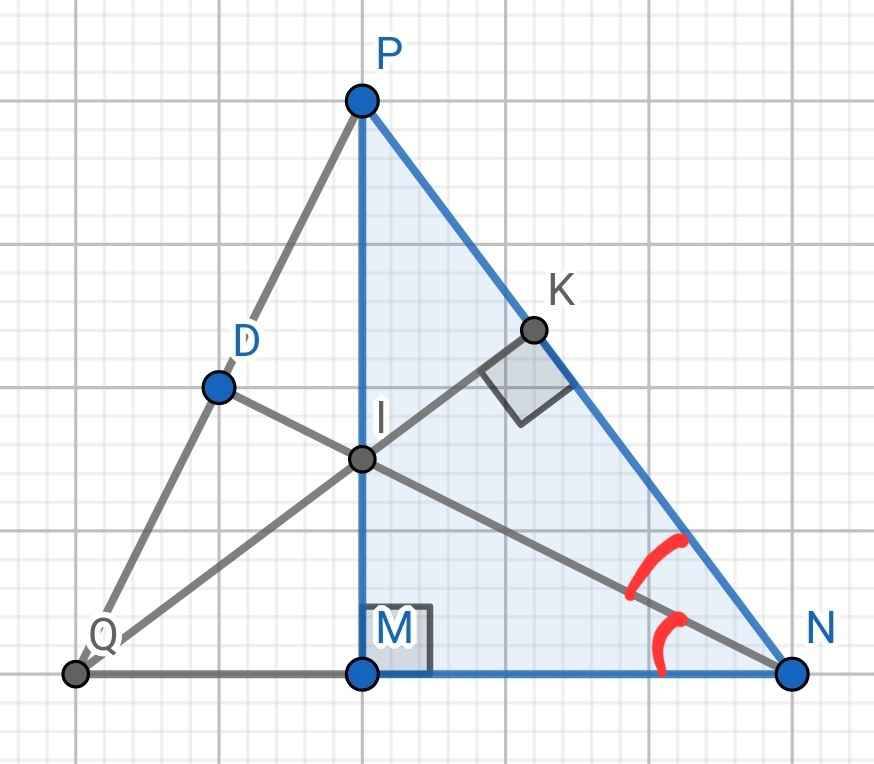
a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:
IN chung
MNI = KNI (do NI là phân giác của ∠MNP)
⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)
b) ∆IKP vuông tại K
IP là cạnh huyền nên IP lớn nhất
IK < IP (1)
Do ∆IMN = ∆IKN (cmt)
⇒ MI = IK (2)
Từ (1) và (2)⇒ MI < IP
c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:
IM = IK (cmt)
∠PIK = ∠MIQ (đối đỉnh)
∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)
⇒ KP = MQ (hai cạnh tương ứng) (3)
Do ∆IMN = ∆IKN (cmt)
⇒ MN = KN (hai cạnh tương ứng) (4)
Từ (3) và (4) ⇒ KN + KP = MN + MQ
NP = NQ
⇒ ∆NPQ cân tại N
Lại có NI là phân giác của ∠MNP
⇒ NI là phân giác của ∠QNP
⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)
⇒ ND ⊥ QP

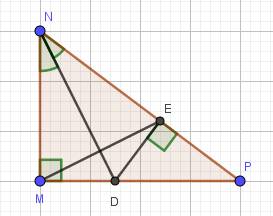
a) Xét hai tam giác vuông: \(\Delta MND\) và \(\Delta END\) có:
ND chung
\(\widehat{MND}=\widehat{END}\) (ND là phân giác của \(\widehat{MNP}\))
\(\Rightarrow\Delta MND=\Delta END\) (cạnh huyền-góc nhọn)
b) Do \(\Delta MND=\Delta END\left(cmt\right)\)
\(\Rightarrow MD=ED\) (hai cạnh tương ứng)
\(\Delta MED\) có MD = ED (cmt)
\(\Rightarrow\Delta MED\) cân tại D
c) Ta có:
\(\widehat{NDP}\) là góc ngoài của \(\Delta MND\)
\(\Rightarrow\widehat{NDP}=\widehat{NMD}+\widehat{MND}\)
\(=90^0+\widehat{MND}\)
\(\Rightarrow\widehat{NDP}\) là góc tù
\(\Delta NDP\) có \(\widehat{NDP}\) là góc tù
Mà góc tù là góc lớn nhất trong tam giác
\(\Rightarrow NP\) là cạnh lớn nhất (quan hệ giữa góc và cạnh đối diện trong \(\Delta NDP\))
\(\Rightarrow ND< NP\)

a: Xét ΔNME có
ND là đường cao
ND là đường phân giác
Do đó: ΔNME cân tại N
b: Xét ΔNMD và ΔNED có
NM=NE
\(\widehat{MND}=\widehat{END}\)
ND chung
DO đó: ΔNMD=ΔNED
Suy ra: DM=DE
mà NM=NE
nên ND là đường trung trực của ME

a: NP^2=MN^2+MP^2
=>ΔMNP vuông tại M
b: Xét ΔNMD vuông tại M và ΔNED vuông tại E có
ND chung
góc MND=góc END
=>ΔNMD=ΔNED
=>DM=DE

a: Xét ΔNMD vuông tại M và ΔNED vuông tại E có
ND chung
góc MND=góc END
=>ΔNMD=ΔNED
=>MN=NE
b: Xét ΔNFP có
PM,FE là đường cao
PM cắt FE tại D
=>D là trực tâm
=>ND vuông góc FP
a: Xét ΔNMK co
NE vừa là đường cao, vừa là phân giác
=>ΔNMK cân tại N
=>NM=NK
Xét ΔNMD và ΔNKD có
NM=NK
góc MND=góc KND
ND chung
=>ΔMND=ΔKND
=>góc NKD=90 độ
=>DK vuông góc NP
b: Xét ΔNKM có
MH,NE là đường cao
MH cắt NE tại I
=>I là trực tâm
=>KI vuông góc MN
=>KI//MP