Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác MDNE có
I là trung điểm chung của MN và DE
góc MDN=90 độ
Do đó: MDNE là hình chữ nhật
b: Xét tứ giác MNFP có
D là trung điểm chung của MF và NP
MN=MP
Do đó: MNFP là hình thoi

a) Xét tam giác MNP:
+ B là trung điểm MN (gt).
+ C là trung điểm MP (gt).
→ BC là đường trung bình.
→ BC // NP (Tính chất đường trung bình).
Xét tứ giác NBCP: BC // NP (cmt).
→ Tứ giác NBCP là hình thang (dhnb).
b) Xét tứ giác MANE:
+ B là trung điểm của MN (gt).
+ B là trung điểm của ED (E là điểm đối xứng của A qua B).
→ Tứ giác MANE là hình bình hành (dhnb).
Mà \(\widehat{MAN}=90^o\) \(\left(MA\perp NP\right).\)
→ Tứ giác MANE là hình chữ nhật (dhnb).

a) Xét tam giác MNP:
+ B là trung điểm MN (gt).
+ C là trung điểm MP (gt).
\(\rightarrow\) BC là đường trung bình.
\(\rightarrow\) BC // NP (Tính chất đường trung bình).
Xét tứ giác NBCP: BC // NP (cmt).
\(\rightarrow\) Tứ giác NBCP là hình thang (dhnb).
b) Xét tứ giác MANE:
+ B là trung điểm của MN (gt).
+ B là trung điểm của ED (E là điểm đối xứng của A qua B).
\(\rightarrow\) Tứ giác MANE là hình bình hành (dhnb).
Mà \(\widehat{MAN}=90^o\left(MA\perp NA\right).\)
\(\rightarrow\) Tứ giác MANE là hình chữ nhật (dhnb).
c) Xét tam giác MNP:
+ C là trung điểm MP (gt).
+ D là trung điểm NP (gt).
\(\rightarrow\) CD là đường trung bình.
\(\rightarrow\) CD // MN (Tính chất đường trung bình).
\(\rightarrow\) \(\widehat{CDP}=\widehat{ANM}\) (Đồng vị).
Mà \(\widehat{ANM}=\widehat{BAN}\) (Tứ giác MANE là hình chữ nhật).
\(\rightarrow\) \(\widehat{CDP}=\widehat{BAN}.\)

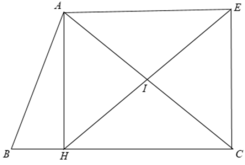
+ Trong Δ AHC vuông có I là trung điểm của AC
⇒ HE là đường trung tuyến của Δ AHC.
⇒ HI = 1/2AC = AI = IC.
Mà E đối xứng với H qua I ⇒ HI = IE.
Khi đó ta có HI = IE = AI = IC.
+ Xét Δ HCE có CI là đường trung tuyến ứng với cạnh HE
mà CI = 1/2HE ⇒ Δ HCE vuông tại C.
Tương tự xét với Δ AHE,Δ AEC đều là các tam giác vuông tại A, E.
Xét tứ giác AHCE có E A H ^ = A H C ^ = H C E ^ = C E A ^ = 90 0
⇒ AHCE là hình chữ nhật.