Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chắc là tam giác này cân tại M, hy vọng thế
\(\Delta AEB=\Delta BDA\left(ch-gn\right)\) \(\Rightarrow\widehat{EBA}=\widehat{DAB}\)
\(\widehat{DAB}=\widehat{ABF}\left(slt\right)\) \(\Rightarrow\widehat{EBA}=\widehat{ABF}\)
\(\Rightarrow BA\) là phân giác góc \(\widehat{EBF}\)
Áp dụng định lý phân giác: \(\frac{AE}{AF}=\frac{BE}{BF}\)

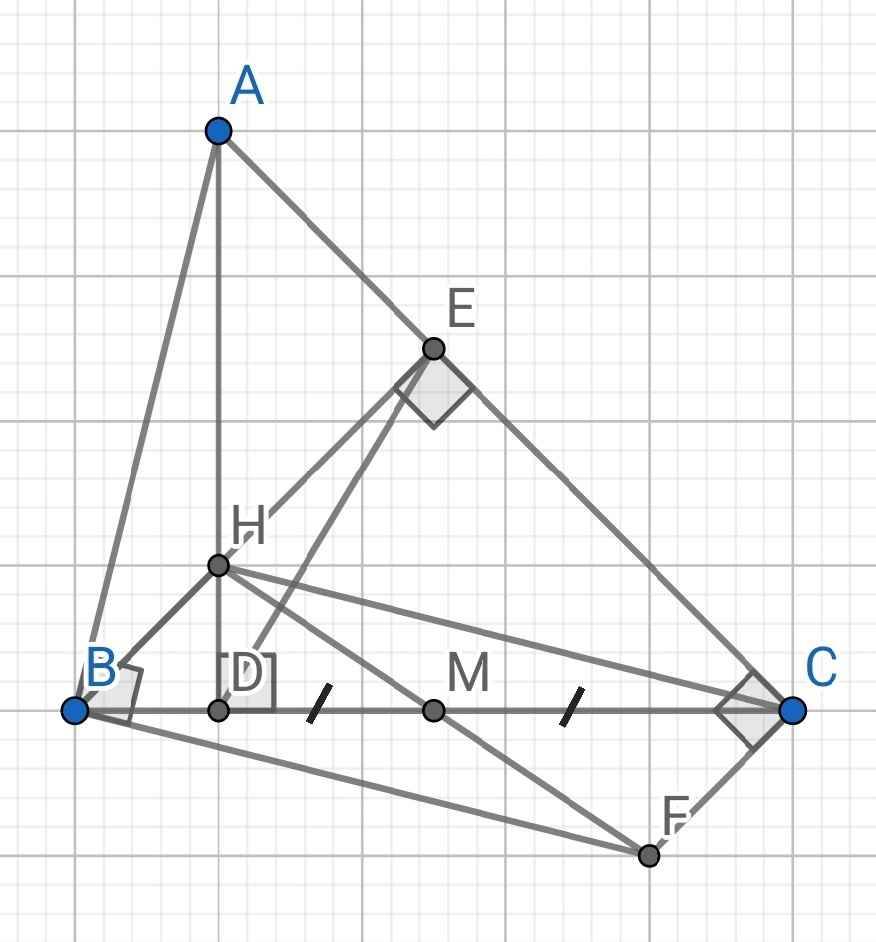 d) Do H là giao điểm của hai đường cao AD và BE của ∆ABC (gt)
d) Do H là giao điểm của hai đường cao AD và BE của ∆ABC (gt)
⇒ CH là đường cao thứ ba của ∆ABC
⇒ CH ⊥ AB
Mà BF ⊥ AB (gt)
⇒ CH // BF
Do CF ⊥ AC (gt)
BE ⊥ AC (gt)
⇒ CF // BE
⇒ CF // BH
Tứ giác BHCF có:
CH // BF (cmt)
CF // BH (cmt)
⇒ BHCF là hình bình hành
e) Do BHCF là hình bình hành (cmt)
Mà M là trung điểm của đường chéo BC (gt)
⇒ M là trung điểm của đường chéo HF
⇒ H, M, F thẳng hàng
Hình chắc có rồi!!
a) Vì MB vuông góc FB => MBF = 90o
Xét tg MAD và tg MFB có
M chung
MDA = MBF ( = 90 )
do đó tg MAD ~ tg MFB => \(\frac{MA}{MD}\)= \(\frac{MF}{MB}\)
=> MA.MB = MD.MF hay MA2 = MD.MF ( vì tg MAB cân => MA = MB )
c nhầm đề không?
Câu C mình gi đúng đề rồi bạn