Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình chắc có rồi!!
a) Vì MB vuông góc FB => MBF = 90o
Xét tg MAD và tg MFB có
M chung
MDA = MBF ( = 90 )
do đó tg MAD ~ tg MFB => \(\frac{MA}{MD}\)= \(\frac{MF}{MB}\)
=> MA.MB = MD.MF hay MA2 = MD.MF ( vì tg MAB cân => MA = MB )
c nhầm đề không?

a) dễ chứng minh tam giác HBA đồng dạng với tam giác ABC
suy ra \(\frac{AB}{BC}=\frac{BH}{AB}\left(1\right)\Rightarrow AB^2=BH\cdot BC\)
b) Xét \(\Delta ABH\)có
BD là đường phân giác của \(\Delta ABH\)
suy ra \(\frac{DH}{DA}=\frac{BH}{AB}\left(2\right)\)
Xét \(\Delta ABC\)có
BE à đường phân giác của \(\Delta ABC\)
suy ra \(\frac{EA}{EC}=\frac{AB}{BC}\left(3\right)\)
từ 1,2,3 suy ra đpcm

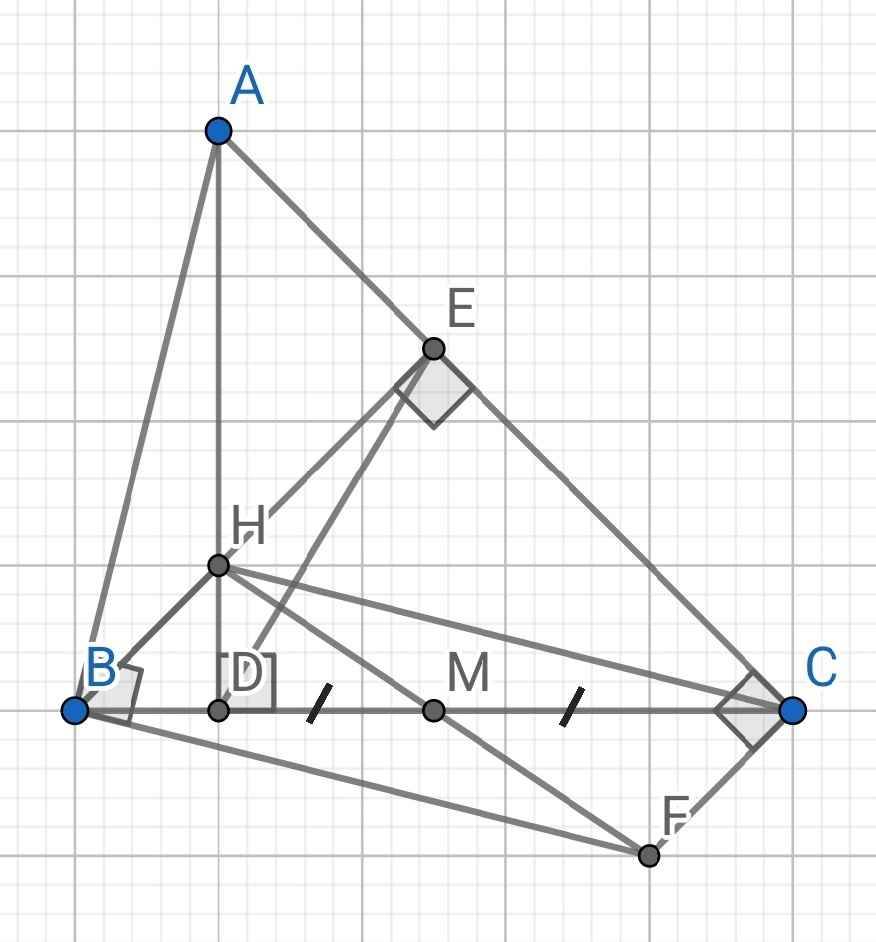 d) Do H là giao điểm của hai đường cao AD và BE của ∆ABC (gt)
d) Do H là giao điểm của hai đường cao AD và BE của ∆ABC (gt)
⇒ CH là đường cao thứ ba của ∆ABC
⇒ CH ⊥ AB
Mà BF ⊥ AB (gt)
⇒ CH // BF
Do CF ⊥ AC (gt)
BE ⊥ AC (gt)
⇒ CF // BE
⇒ CF // BH
Tứ giác BHCF có:
CH // BF (cmt)
CF // BH (cmt)
⇒ BHCF là hình bình hành
e) Do BHCF là hình bình hành (cmt)
Mà M là trung điểm của đường chéo BC (gt)
⇒ M là trung điểm của đường chéo HF
⇒ H, M, F thẳng hàng
Chắc là tam giác này cân tại M, hy vọng thế
\(\Delta AEB=\Delta BDA\left(ch-gn\right)\) \(\Rightarrow\widehat{EBA}=\widehat{DAB}\)
\(\widehat{DAB}=\widehat{ABF}\left(slt\right)\) \(\Rightarrow\widehat{EBA}=\widehat{ABF}\)
\(\Rightarrow BA\) là phân giác góc \(\widehat{EBF}\)
Áp dụng định lý phân giác: \(\frac{AE}{AF}=\frac{BE}{BF}\)
Tưởng m lớp 9 hay 10 gì chứ -_-