Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

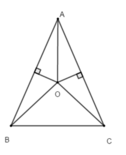
+ Vì O thuộc đường trung trực của AB nên OA = OB, do đó đáp án A sai
+ Vì ba đường trung trực của tam giác đồng quy tại một điểm nên O là giao điểm của ba đường trung trực của tam giác ABC, suy ra O thuộc đường trung trực cạnh BC
Mà AB = AC nên A thuộc đường trung trực cạnh BC
Do đó AO là đường trung trực của BC ⇒ A O ⊥ B C , nên đáp án C đúng
+ Lại có tam giác ABC cân tại A (AB = AC) có AO là trung trực nên AO cũng là phân giác của góc BAC ⇒ B A O ^ = C A O ^
Khi đó Δ B A O = Δ C A O ( c – g – c) (vì AB = AC, AO chung, B A O ^ = C A O ^ )
Suy ra A O B ^ = A O C ^ ⇒ Đáp án B sai
+ Do tam giác ABC là tam giác cân không đều nên O không phải là giao điểm của ba đường phân giác trong tam giác ABC nên O không cách đều ba cạnh của tam giác ABC, do đó đáp án D sai.
Chọn đáp án C


+ Vì G là trọng tâm của tam giác ABC có AD là một trung tuyến nên AG = 2/3AD, suy ra G không thể là trung điểm của AD => B sai
+ Vì AG = 2/3 AD => GD = 1/3 AD
Mà DM = 1/3 AD nên GD = DM
Mặt khác G thuộc tia DA, M thuộc tia đối của tia DA nên D nằm giữa M và G
Do đó D là trung điểm của MG, nên A đúng.


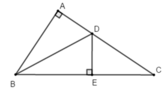
Từ D kẻ đường thẳng vuông góc với BC cắt BC tại E
Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
BD cạnh huyền chung
A B D ^ = E B D ^ (BD là tia phân giác của góc B)
Khi đó: Δ A B D = Δ E B D (cạnh huyền góc nhọn)
Suy ra: AD = DE (hai cạnh tương ứng) (1)
Lại có tam giác DEC vuông tại E có DC là cạnh huyền
Suy ra DC > DE (trong tam giác vuông, cạnh đối diện với góc vuông là cạnh lớn nhất) (2)
Từ (1) và (2) suy ra DC > AD hay AD < DC
Vậy A đúng, B, C, D sai.
Chọn đáp án A
