Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

AB=AC
OB=OC
=>AO là trug trực của BC
=>AD là trung trực của BC
=>AD là phân giác của góc BAC
=>góc BAD=1/2*60=30 độ
=>góc BMD=30 độ

AB=AC
OB=OC
=>AO là trug trực của BC
=>AD là trung trực của BC
=>AD là phân giác của góc BAC
=>góc BAD=1/2*60=30 độ
=>góc BMD=30 độ

a: góc AHM+góc AKM=180 độ
=>AHMK nội tiếp
b: Xét ΔMHB vuông tại H và ΔMKC vuông tại K có
góc HBM=góc KCM
=>ΔMHB đồng dạng vơi ΔMKC
=>MH/MK=MB/MC
=>MH*MC=MB*MK

a/ Trọng tâm của tam giác cũng là tâm của đường tròn nội tiếp và ngoại tiếp.
ΔABC đều, AD là đường kính cũng là tia phân giác của góc BAC
⇒ góc BAD = góc DAC ⇒ cung BD = cung DC
⇒ góc BMD = góc DMC ⇒ MD là tia phân giác góc BMC.
b/
ΔACD vuông tại C (do nội tiếp dường tròn đường kính AD = 2R) có góc DAC =1/2 góc BAC = 30º nên là nửa tam giác đều ⇒ AC = R√3, DC = R
Diện tích ΔACD: 1/2AC*CD = 1/2R√3*R = √3R² /2
ΔACD = ΔABD (c.g.c) ⇒ dthtABCD =2dtΔACD = 2*√3R² /2 = √3R²
c/
Gọi I là giao điểm của AM và DB
góc ABD = góc AMD = 90º (2góc nội tiếp đường tròn đk AD)
⇒ AB, DM là hai đường cao của ΔIAD
K là trực tâm của tam giác nên IK ⊥ AD (1)
AC=AB ⇒ cung AC = cung AB ⇒ góc AMC = góc ADB hay góc AMH = góc HDI
góc AMH kề bù với góc HMI nên góc HMI + góc HDI = 180º
⇒ tứ giác IMHD nội tiếp đường tròn đường kính ID.
⇒ góc IMD = góc IHD = 90º
⇒ IH ⊥ AD (2)
Từ (1),(2) ⇒ I, H, K thẳng hàng
hay ba đường thẳng AM, BD, HK đồng quy tại I.

a:góc AHM+góc AKM=180 độ
=>AHMK nội tiếp
b: góc MBH+góc ABM=180 độ
góc MCK+góc ACM=180 độ
góc ABM=góc ACM
=>góc MBH=góc MCK
mà góc MHB=góc MKC
nên ΔMHB đồng dạng vơi ΔMKC
=>MH/MK=MB/MC
=>MH*MC=MK*MB

a: góc AHM+góc AKM=180 độ
=>AHMK là tứ giác nội tiếp
b: góc HBM=180 độ-góc ABM
góc KCM=180 độ-góc ACM
góc ABM=góc ACM
=>góc HBM=góc KCM
mà góc MHB=góc MKC
nên ΔMBH đồng dạng với ΔMCK
=>MB/MC=MH/MK
=>MB*MK=MC*MH

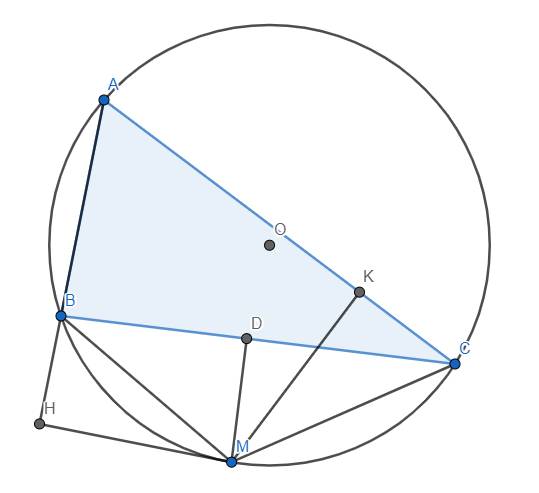
a) Theo đề bài, ta thấy \(\widehat{AHM}=\widehat{AKM}=90^o\) nên dễ dàng suy ra tứ giác AHMK nội tiếp do 2 góc đối bù nhau.
b) Do tứ giác AHMK nội tiếp nên \(\widehat{HMK}+\widehat{A}=180^o\). Tứ giác ABMC nội tiếp nên \(\widehat{BMC}+\widehat{A}=180^o\). Từ đó suy ra \(\widehat{HMK}=\widehat{BMC}\) hay \(\widehat{BMH}=\widehat{CMK}\). Lại có \(\widehat{MHB}=\widehat{MKC}=90^o\) nên \(\Delta MHB~\Delta MKC\left(g.g\right)\) \(\Rightarrow\dfrac{MH}{MK}=\dfrac{MB}{MC}\) \(\Rightarrowđpcm\)
\(\widehat{BMD}=\widehat{BAD}\) (cùng chắn cung BD)
Tam giác ABD vuông tại B (do AD là đường kính)
\(\Rightarrow\widehat{BAD}=90^0-\widehat{BDA}\)
Mà \(\widehat{BDA}=\widehat{BCA}=60^0\) (cùng chắn cung AB và tam giác ABC đều nên \(\widehat{BCA}=60^0\))
\(\Rightarrow\widehat{BMD}=\widehat{BAD}=90^0-60^0=30^0\)
AB=AC
OB=OC
=>AO là trug trực của BC
=>AD là trung trực của BC
=>AD là phân giác của góc BAC
=>góc BAD=1/2*60=30 độ
=>góc BMD=30 độ