Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Xét tam giác DEH và tam giác DFH ta có:
DE = DF ( tam giác DEF cân tại D )
DEH = DFH ( tam giác DEF cân tại D )
EH = EF ( H là trung điểm của EF )
=> tam giác DEH = tam giác DFH ( c.g.c) (dpcm)
=> DHE=DHF(hai góc tương ứng)
Mà DHE+DHF=180 độ =>DHE=DHF=180 độ / 2 = 90 độ ( góc vuông ) hay DH vuông góc với EF ( dpcm )
b) Xét tam giác MEH và tam giac NFH ta có:
EH=FH(theo a)
MEH=NFH(theo a)
=> tam giác MEH = tam giác NFH ( ch-gn)
=> HM=HN ( 2 cạnh tương ứng ) hay tam giác HMN cân tại H ( dpcm )
c) Ta có : +) DM+ME=DE =>DM=DE-ME
+) DN+NF=DF => DN=DF-NF
Mà DE=DF(theo a) ; ME=NF( theo b tam giác MEH=tam giác NFH)
=>DM=DN => tam giác DMN cân tại D
Xét tam giac cân DMN ta có:
DMN=DNM=180-MDN/2 (*)
Xét tam giác cân DEF ta có:
DEF=DFE =180-MDN/2 (*)
Từ (*) và (*) Suy ra góc DMN = góc DEF
Mà DMN và DEF ở vị trí đồng vị
=> MN//EF (dpcm)
d) Xét tam giác DEK và tam giác DFK ta có:
DK là cạnh chung
DE=DF(theo a)
=> tam giác DEK= tam giác DFK(ch-cgv)
=>DKE=DKF(2 góc tương ứng)
=>DK là tia phân giác của góc EDF (1)
Theo a tam giac DEH= tam giac DFH(c.g.c)
=>EDH=FDH(2 góc tương ứng)
=>DH là tia phân giác của góc EDF (2)
Từ (1) và (2) Suy ra D,H,K thẳng hàng (dpcm)
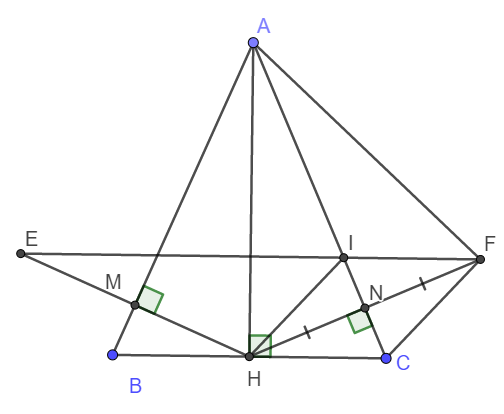
a) Do ABC là tam giác cân tại A nên AH là đường cao hay đồng thời là đường phân giác.
Xét tam giác vuông AMH và tam giác vuông ANH có:
Cạnh AH chung
\(\widehat{MAH}=\widehat{NAH}\)
\(\Rightarrow\Delta AMH=\Delta ANH\) (Cạnh huyền - góc nhọn)
\(\Rightarrow HM=HN.\)
b) Dễ dàng thấy ngay AC là đường trung trực của HF.
Khi đó thì AH = AF; CH = CF
Xét tam giác AHC và tam giác AFC có:
Cạnh AC chung
AH - AF
CH = CF
\(\Rightarrow\Delta AHC=\Delta AFC\left(c-c-c\right)\)
\(\Rightarrow\widehat{AFC}=\widehat{AHC}=90^o\Rightarrow AF\perp CF.\)
c) Ta thấy ngay \(\Delta HIN=\Delta FCN\left(g-c-g\right)\)
\(\Rightarrow IN=CN\)
Xét tam giác vuông INF và tam giác vuông CNH có:
HN = FN
IN = CN
\(\Rightarrow\Delta INF=\Delta CNH\) (Hai cạnh góc vuông)
\(\Rightarrow\widehat{IFN}=\widehat{CHN}\)
Mà chúng lại ở vị trí so le trong nên IF // BC.
d) Chứng minh tương tự câu c, ta có IE // BC
Vậy thì qua I có hai tia IE và IF cùng song song với BC nên chúng trùng nhau.
Vậy I, E, F thẳng hàng.
A B C H F N I M E
a) Xét \(\Delta ABH,\Delta ACH\) có :
\(\widehat{ABH}=\widehat{ACH}\) (\(\Delta ABC\) cân tại A)
\(AB=AC\) (\(\Delta ABC\) cân tại A)
\(\widehat{AHB}=\widehat{AHC}\left(=90^o\right)\)
=> \(\Delta ABH=\Delta ACH\) (cạnh huyền - góc nhọn)
=> HB= HC (2 cạnh tương ứng)
Xét \(\Delta MBH,\Delta NCH\) có :
\(\widehat{MBH}=\widehat{KCH}\) (\(\Delta ABC\) cân tại A)
\(BH=CH\left(cmt\right)\)
\(\widehat{BMH}=\widehat{CNH}\left(=90^o\right)\)
=> \(\Delta MBH=\Delta NCH\) (cạnh huyền - góc nhọn)
=> HM = HN (2 cạnh tương ứng)
b) Xét \(\Delta AHN,\Delta AHF\) có :
\(NH=FN\left(gt\right)\)
\(\widehat{ANH}=\widehat{ANF}\left(=90^o\right)\)
\(AN:Chung\)
=> \(\Delta AHN=\Delta AHF\left(c.g.c\right)\)
Xét \(\Delta HNC,\Delta FNC\) có :
\(\widehat{HNC}=\widehat{FNC}\left(=90^o\right)\)
\(NC:Chung\)
\(HN=FN\left(gt\right)\)
=> \(\Delta HNC=\Delta FNC\left(c.g.c\right)\)
Ta có : \(\widehat{AHN}+\widehat{NHC}=90^o\)
Mà : \(\left\{{}\begin{matrix}\widehat{AHN}=\widehat{AKN}\\\widehat{NHC}=\widehat{NFC}\end{matrix}\right.\)
Nên : \(\widehat{AFN}+\widehat{NFC}=90^o\)
Hay : \(\widehat{AFC}=90^o\)
\(\Leftrightarrow FC\perp AF\)
A B C D H E F M N
CM: a) Xét t/giác ABM và t/giác ACN
có: AB = AC (gt)
\(\widehat{B}=\widehat{C}\) (vì t/giác ABC cân)
BM = CN (gt)
=> t/giác ABM = t/giác ACN (c.g.c)
b) Ta có: BM + MD = BD
CN + ND = CD
Mà BM = CN (gt); MD = ND (gt)
=> BD = CD
Xét t/giác ABD và t/giác ACD
có: AB = AC (gt)
\(\widehat{B}=\widehat{C}\) (vì t/giác ABC cân)
BD = CD (cmt)
=> t/giác ABD = t/giác ACD (c.g.c)
=> \(\widehat{BAD}=\widehat{CAD}\) (2 góc t/ứng)
=> AD là tia p/giác của \(\widehat{BAC}\)
c) Xét t/giác MEB = t/giác NFC
có: \(\widehat{BEM}=\widehat{CFN}=90^0\) (gt)
BM = CN (gt)
\(\widehat{B}=\widehat{C}\) (vì t/giác ABC cân)
=> t/giác MEB = t/giác NFC (ch - gn)
d) Ta có: AB = AE + EB
AC = AF + FA
mà AB = AC (gt); EB = FC (vì t/giác MEB = t/giác NFC)
=> AE = AF
=> t/giác AEF cân tại A
=> \(\widehat{AEF}=\widehat{AFE}=\frac{180^0-\widehat{A}}{2}\) (1)
T/giác ABC cân tại A
=> \(\widehat{B}=\widehat{C}=\frac{180^0-\widehat{A}}{2}\) (2)
Từ (1) và (2) => \(\widehat{AEF}=\widehat{B}\)
Mà 2 góc này ở vị trí đồng vị
=> EF // BC
e) Xét t/giác AEH và t/giác AFH
có: AE = AF (cmt)
\(\widehat{AEH}=\widehat{AFH}=90^0\) (gt)
AH : chung
=> t/giác AEH = t/giác AFH (ch - cgv)
=> \(\widehat{EAH}=\widehat{FAH}\) (2 góc t/ứng)
=> AH là tia p/giác của \(\widehat{A}\)
Mà AD cũng là tia p/giác của \(\widehat{A}\)
=> AH \(\equiv\) AD
=> A, D, H thẳng hàng
M: a) Xét t/giác ABM và t/giác ACN
có: AB = AC (gt)
�^=�^B=C (vì t/giác ABC cân)
BM = CN (gt)
=> t/giác ABM = t/giác ACN (c.g.c)
b) Ta có: BM + MD = BD
CN + ND = CD
Mà BM = CN (gt); MD = ND (gt)
=> BD = CD
Xét t/giác ABD và t/giác ACD
có: AB = AC (gt)
�^=�^B=C (vì t/giác ABC cân)
BD = CD (cmt)
=> t/giác ABD = t/giác ACD (c.g.c)
=> ���^=���^BAD=CAD (2 góc t/ứng)
=> AD là tia p/giác của ���^BAC
c) Xét t/giác MEB = t/giác NFC
có: ���^=���^=900BEM=CFN=900 (gt)
BM = CN (gt)
�^=�^B=C (vì t/giác ABC cân)
=> t/giác MEB = t/giác NFC (ch - gn)
d) Ta có: AB = AE + EB
AC = AF + FA
mà AB = AC (gt); EB = FC (vì t/giác MEB = t/giác NFC)
=> AE = AF
=> t/giác AEF cân tại A
=> ���^=���^=1800−�^2AEF=AFE=21800−A (1)
T/giác ABC cân tại A
=> �^=�^=1800−�^2B=C=21800−A (2)
Từ (1) và (2) => ���^=�^AEF=B
Mà 2 góc này ở vị trí đồng vị
=> EF // BC
e) Xét t/giác AEH và t/giác AFH
có: AE = AF (cmt)
���^=���^=900AEH=AFH=900 (gt)
AH : chung
=> t/giác AEH = t/giác AFH (ch - cgv)
=> ���^=���^EAH=FAH (2 góc t/ứng)
=> AH là tia p/giác của �^A
Mà AD cũng là tia p/giác của �^A
=> AH ≡≡ AD
=> A, D, H thẳng hàng
\(a,\left\{{}\begin{matrix}\widehat{F}+\widehat{E}=90^0\\\widehat{HDE}+\widehat{E}=90^0\end{matrix}\right.\Rightarrow\widehat{F}=\widehat{HDE}\\ b,\left\{{}\begin{matrix}\widehat{F}+\widehat{E}=90^0\\\widehat{HDF}+\widehat{F}=90^0\end{matrix}\right.\Rightarrow\widehat{E}=\widehat{HDF}\)