Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: MK\(\perp\)PQ; MN\(\perp\)PR
a: ta có: ΔPQR vuông tại P
=>\(QR^2=PQ^2+PR^2\)
=>\(QR^2=8^2+6^2=100\)
=>\(QR=\sqrt{100}=10\left(cm\right)\)
Ta có: ΔRPQ vuông tại P
mà PM là đường trung tuyến
nên \(PM=\dfrac{RQ}{2}=5\left(cm\right)\)
b: Xét tứ giác PNMK có
\(\widehat{PNM}=\widehat{PKM}=\widehat{NPK}=90^0\)
=>PNMK là hình chữ nhật
c: Xét ΔRPQ có
M là trung điểm của RQ
MK//RP
Do đó: K là trung điểm của PQ
=>PK=KQ(1)
Ta có: PKMN là hình chữ nhật
=>PK=MN(2)
Từ (1) và (2) suy ra KQ=MN
Ta có: PK//MN
K\(\in\)PQ
Do đó: NM//KQ
Xét tứ giác KQMN có
KQ//MN
KQ=MN
Do đó: KQMN là hình bình hành
=>QN cắt MK tại trung điểm của mỗi đường
mà O là trung điểm của MK
nên O là trung điểm của QN
=>OQ=ON
Xét tứ giác PMQH có
K là trung điểm chung của PQ và MN
=>PMQH là hình bình hành
Hình bình hành PMQH có PQ\(\perp\)MH
nên PMQH là hình thoi

P Q R M N
Ta có: $PQ=PM+MQ$\(\Rightarrow PM=PQ-MQ=8-6=2\left(cm\right)\)
Áp dụng định lý Thales trong tam giác PQR, có:
\(\frac{PM}{PQ}=\frac{PN}{PR}\Leftrightarrow PR=\frac{PN.PQ}{PM}=\frac{3.8}{2}=12\left(cm\right)\)
KL: .........................

a: Xét ΔPQR có
E là trung điểm của PQ
F là trung điểm của PR
DO đó: EF là đường trung bình
=>EF//QR và EF=QR/2
=>EF//QG và EF=QG
Xét tứ giác QEFR có EF//QR
nên QEFR là hình thang
b: EF=QR/2=16/2=8(cm)
c: Xét tứ giác EFGQ có
EF//GQ
EF=GQ
Do đó: EFGQ là hình bình hành

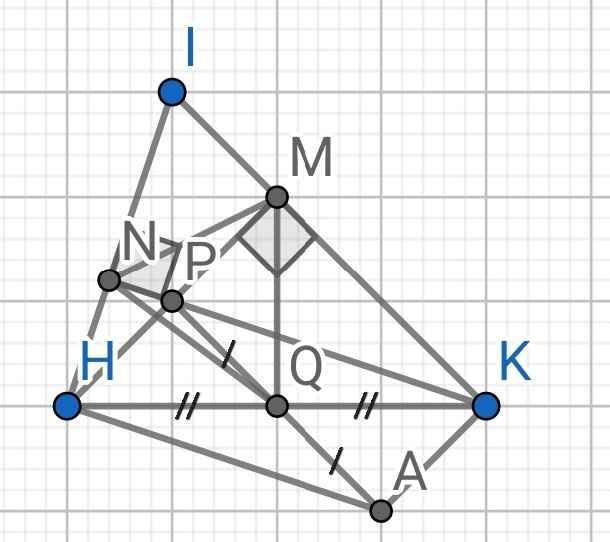 a) Do PQ = QA (gt)
a) Do PQ = QA (gt)
⇒ Q là trung điểm của AP
Tứ giác PHAK có:
Q là trung điểm của AP (cmt)
Q là trung điểm của HK (gt)
⇒ PHAK là hình bình hành
b) Do PHAK là hình bình hành (cmt)
⇒ PK = AH
c) ∆HNK vuông tại N
Q là trung điểm của HK (gt)
⇒ NQ là đường trung tuyến ứng với cạnh huyền HK
⇒ NQ = HK : 2 (1)
∆HMK vuông tại M
Q là trung điểm HK (gt)
⇒ MQ là đường trung tuyến ứng với cạnh huyền HK
⇒ MQ = HK : 2 (2)
Từ (1) và (2) ⇒ MQ = NQ
∆MNQ có:
MQ = NQ (cmt)
⇒ ∆MNQ cân tại Q

Câu 1:
1. Vì $P,Q$ lần lượt là trung điểm của $AB,AC$ nên $PQ$ là đường trung bình của tam giác $ABC$ ứng với $BC$
$\Rightarrow PQ=\frac{1}{BC}=MC$ và $PQ\parallel BC$ hay $PQ\parallel MC$
Tứ giác $PQCM$ có cặp cạnh đối $PQ$ và $MC$ vừa song song vừa bằng nhau nên $PQCM$ là hình bình hành.
2.Vì tam giác $ABC$ cân tại $A$ nên đường trung tuyến $AM$ đồng thời là đường cao. Hay $AM\perp BC$
Tứ giác $NAMB$ có 2 đường chéo $MN, AB$ cắt nhau tại trung điểm $P$ của mỗi đường nên $NAMB$ là hình bình hành.
Hình bình hành $NAMB$ có 1 góc vuông ($\widehat{AMB}$) nên $NAMB$ là hình vuông.
$\Rightarrow NB\perp BM$ hay $NB\perp BC$ (đpcm)
3.
Vì $PQCM$ là hình bình hành nên $PM\parallel QC; PM=QC$. Mà $P,M,N$ thẳng hàng; $PM=PN$ nên $PN\parallel QC$ và $PN=QC$
Tứ giác $PNQC$ có cặp cạnh đối $PN, QC$ song song và bằng nhau nên $PNQC$ là hình bình hành.
Do đó $PC\parallel QN(1)$
Mà $PC\parallel QF$ (2)
Từ $(1);(2)\Rightarrow Q,N,F$ thẳng hàng (đpcm)

tham khảo nha bạn :))
b) Ta đã chứng minh được tứ giác BCNM là hình thang cân, suy ra N là trung điểm của đáy BC.
câu b nha

A B C D M N E Q F P K S
a) Dễ thấy PE là đường trung bình của \(\Delta ABD\)\(\Rightarrow PE=\frac{1}{2}BD\)
Tương tự : \(QE=\frac{1}{2}AC;QF=\frac{1}{2}BD;PF=\frac{1}{2}AC\)
Theo bài toán, BD = AC nên \(PE=EQ=QF=PF\)
Suy ra PEQF là hình thoi
b) Gọi K là trung điểm của BD . Đường thẳng ME cắt NF tại S
Vì PEQF là hình thoi nên \(EF\perp PQ\)( * )
Xét \(\Delta KQP\)và \(\Delta SFE\)có :
\(ME\perp AB\) ; \(PK//AB\)\(\Rightarrow ME\perp PK\)
Tương tự : \(NF\perp QK\)
\(\Rightarrow\Delta KQP\approx\Delta SFE\)( góc có cạnh tương ứng vuông góc )
\(\Rightarrow\frac{SE}{SF}=\frac{KP}{KQ}=\frac{AB}{CD}\)( 1 )
Vì \(\Delta MAB\approx\Delta NCD\Rightarrow\frac{AB}{CD}=\frac{ME}{NF}\)( tỉ số đồng dạng bằng tỉ số đường cao ) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra : \(\frac{SE}{SF}=\frac{ME}{NF}\Rightarrow EF//MN\)( ** )
Từ ( * ) và ( ** ) suy ra : \(PQ\perp MN\)
Gọi E và F là trung điểm của AB và DC tương ứng.
Ta cm 2 vấn đề sau:
1) EF vuông góc với PQ
2) EF // MN
Sơ lược hướng đi là như vậy nha, mai chị sẽ đăng bài cụ thể nhé
Hình vẽ thì bạn tự dựng nha.
Gọi E,F là trung điểm của AB,CD tương ứng
Lần lượt cm các điều sau:
Tương tự:
Cộng theo vế (1) và (2) suy ra
Hình tự vẽ nha!
Vì PQ=PR suy ra tg PQR cân tại P
suy ra : góc PQR=\(\frac{180-P}{2}\)(180 độ, góc P)(1)
Ta có PQ=PR và PM=PN(gt)
vì PM=PN suy ra tg PMN cân tại P
suy ra : góc PMN=\(\frac{180-P}{2}\)(2)
Từ (1),(2) ta có :góc PQR= góc PMN
mà 2 góc ở vị trí đồng vị suy ra MN // QR
suy ra QMNR là hình thang (3)
Vì PQ=PR và PM=PN
suy ra PQ-PM = PR-PN
suy ra MQ=NR(4)
TỪ (3) (4) suy ra QMNR là hình thang cân.