Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

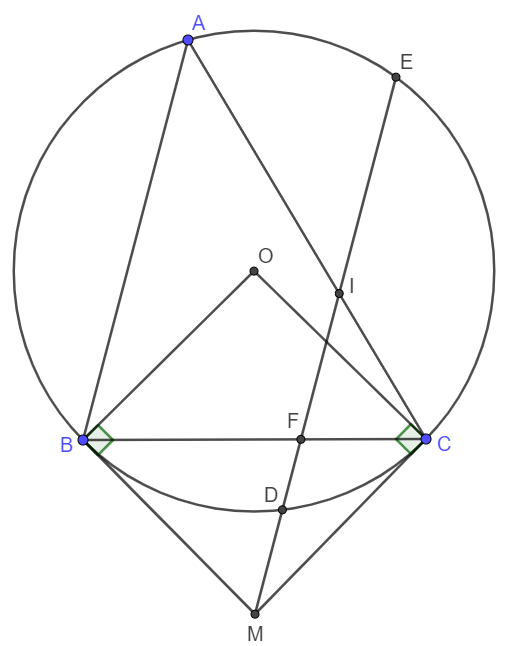
Cho tam giác ABCABC không có góc tù (AB < AC)(AB<AC), nội tiếp đường tròn (O; R)(O;R), (BB, CC cố định, AA di động trên cung lớn BC). Các tiếp tuyến tại BB và CC cắt nhau tại MM. Từ MM kẻ đường thẳng song song với ABAB, đường thẳng này cắt (O)(O) tại DD và EE (DD thuộc cung nhỏ BCBC), cắt BCBC tại FF, cắt ACAC tại II. Chứng minh rằng \widehat{MBC}=\widehat{BAC}MBC=BAC . Từ đó suy ra MBICMBIC là tứ giác nội tiếp.
theo gt, ta co:
goc MBC= BAC (cung chan cung BC)
mat khac, ta lai co goc BAC = MIC ( dong vi)
=> goc MBC= MIC
=> tu giac BICM noi tiep

Bạn tham khảo bài tại link :
https://olm.vn/hoi-dap/detail/244883081409.html
hoặc :
Câu hỏi của Vũ Nguyễn Phương Thảo - Toán lớp 8 - Học trực tuyến OLM
Hok tốt

a)Có :\(\widehat{EBD}=\widehat{BAD}\)(cùng chắn \(\stackrel\frown{BD}\))
\(\widehat{BED}\):chung
\(\Rightarrow\Delta EBD\sim\Delta EAB\left(gg\right)\)
\(\Rightarrow\dfrac{BE}{ED}=\dfrac{EA}{BE}\)\(\Rightarrow EB^2=ED.EA\)(đpcm)
Xét \(\Delta EDC\) và \(\Delta EAC\), có:
\(\widehat{DEC}\):chung;
\(\widehat{ECD}=\widehat{DAC}\)(cùng chắn \(\stackrel\frown{CD}\))
\(\Rightarrow\Delta EDC\sim\Delta ECA\left(gg\right)\)
\(\Rightarrow\dfrac{ED}{EC}=\dfrac{CD}{AC}\)và EB=EC(t/c 2 tt cắt nhau)
Có \(\Delta EBD\sim\Delta EAB\)
\(\Rightarrow\dfrac{BD}{AB}=\dfrac{ED}{EB}\)
\(\Rightarrow\dfrac{CD}{AC}=\dfrac{ED}{EB}=\dfrac{BD}{AB}\Rightarrow\dfrac{AB}{BD}=\dfrac{AC}{CD}\)
b)Có ABDC nt( \(A,B,D,C\in\left(O\right)\))(1)
Có xy//d(gt)
\(\Rightarrow\widehat{xAP}=\widehat{BPE}\)(SLT)
Có \(\widehat{ADB}=\widehat{xAP}\)(cùng chắn \(\stackrel\frown{AB}\))
\(\Rightarrow\widehat{BPE}=\widehat{ADB}\)\(\Rightarrow\)BDEP nt\(\Rightarrow B,D,E,P\)thuộc 1 đường tròn(2)
Có xy//d
\(\Rightarrow\widehat{CAy}=\widehat{CQE}\)(SLT)
Có: \(\widehat{CAy}=\widehat{ADC}\)(cùng chắn \(\stackrel\frown{AC}\))
\(\Rightarrow\widehat{CQE}=\widehat{ADC}\Rightarrow\)CDEQ nt\(\Rightarrow\)C,D,E,Q thuộc 1 đường tròn(3).
Từ (1),(2),(3)\(\Rightarrow\)Đường tròn ngoại tiếp (ABDC),(BDEP),(CDEQ) cùng đi qua D.
Mà tâm đường tròn ngoại tiếp (ABDC) cũng là tâm đường tròn ngoại tiếp (ABC).
Mà tâm đường tròn ngoại tiếp (BDEP) cũng là tâm đường tròn ngoại tiếp (BEP).
Mà tâm đường tròn ngoại tiếp (CDEQ) cũng là tâm đường tròn ngoại tiếp (CEQ).
Vậy đường tròn ngoại tiếp (ABC),(BEP).(CEQ) cùng đi qua D.
Giải gấp em câu d) ạ.
AB // CD
\(\Rightarrow\dfrac{OC}{OA}=\dfrac{CD}{AB}\left(\text{hệ}-\text{quả}-talet\right)\)
\(\Rightarrow\dfrac{CD}{AB+CD}=\dfrac{OC}{OA+OC}=\dfrac{OC}{AC}\)
OE // AB
\(\Rightarrow\dfrac{OE}{AB}=\dfrac{OC}{AC}=\dfrac{CD}{AB+CD}\)
\(\Rightarrow OE=\dfrac{AB\times CD}{AB+CD}\)
\(\Rightarrow\dfrac{1}{OE}=\dfrac{AB+CD}{AB\times CD}=\dfrac{1}{AB}+\dfrac{1}{CD}\left(\text{đ}pcm\right)\)
các bạn ơi các bạn có vẽ được hìnhg không mình không vẽ nổi nen mới hỏi