Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn vẽ hình ra nhé!
Do tam giác ABD vuông cân tại A => góc DAM + góc BAH = 90º. Trong tam giác vuông ABH có góc ABH + góc BAH = 90º => góc DAM = góc ABH (cùng phụ với một góc bằng nhau)
Xét tam giác vuông ADM và tam giác vuông BAH có:
AD = AB (gt)
góc DAM = góc ABH (cmt)
=> tam giác ADM = tam giác BAH (cạnh huyền - góc nhọn)
=> DM = AH
Cmtt ta có: tam giác ANE = tam giác CHA => EN = AH
=> DM = EN (cùng bằng AH)
Lại có: DM // EN (cùng _|_ AH) mà DM = EN (cmt) => tứ giác DMEN là hình bình hành => MN cắt DE tại trung điểm mỗi đường hay MN đi qua trung điểm của DE.
Chúc bạn học giỏi!
tk nha bạn
thank you bạn
(^_^)
Do tam giác ABD vuông cân tại A => góc DAM + góc BAH = 90º. Trong tam giác vuông ABH có góc ABH + góc BAH = 90º => góc DAM = góc ABH (cùng phụ với một góc bằng nhau)
Xét tam giác vuông ADM và tam giác vuông BAH có:
AD = AB (gt)
góc DAM = góc ABH (cmt)
=> tam giác ADM = tam giác BAH (cạnh huyền - góc nhọn)
=> DM = AH
Cmtt ta có: tam giác ANE = tam giác CHA => EN = AH
=> DM = EN (cùng bằng AH)
Lại có: DM // EN (cùng _|_ AH) mà DM = EN (cmt) => tứ giác DMEN là hình bình hành => MN cắt DE tại trung điểm mỗi đường hay MN đi qua trung điểm của DE.

Ta có: ∠(BAH) +∠(BAD) +∠(DAM) =180o(kề bù)
Mà ∠(BAD) =90o⇒∠(BAH) +∠(DAM) =90o(1)
Trong tam giác vuông AMD, ta có:
∠(AMD) =90o⇒∠(DAM) +∠(ADM) =90o(2)
Từ (1) và (2) suy ra: ∠(BAH) =∠(ADM)
Xét hai tam giác vuông AMD và BHA, ta có:
∠(BAH) =∠(ADM)
AB = AD (gt)
Suy ra: ΔAMD= ΔBHA(cạnh huyền, góc nhọn)
Vậy: AH = DM (hai cạnh tương ứng) (3)

a, có góc ADM+DAM=90độ
có góc DAM+DAB+BAH=90độ
=>DAM+BAH=90 độ=>BAH=ADM
có DAM+ADM=90 độ
có BAH+ABH=90 độ
mà ADM=BAH=>ABH=DAM
xét tg DAM và tg BAH
AB=AD
góc ADM=BAH => tg DAM=tg ABH(g.c.g)
góc DAM=ABH
=> DM=AH(2 cạnh t/ứ)
b, nối D,E
xét tg NEA và tg AHC giống ý a, rùi có NE=AH mà DM=AH => DM=NE
gọi giao điểm của DE và NA là T => NTE=DTM(đối đỉnh)
Xét tg MDT và tg NET
NE=DM
NET=TDM(2 góc kia = nhau thì góc này =) => tgMTD=tgNET(g.c.g)
ENT=DMT(=90 độ)
=> DT=ET(2 cạnh t.ứ)=> MN đi qua trung điểm của DE
c, có EAC=DAB(=90độ)=> EAC+BAC=DAB+BAC(1)
DA=BA(2), CA=EA(3)
từ 1,2 3 => 2 tg đó = nhau

Ta có: ∠(HAC) +∠(CAE) +∠(EAN) =180o(kề bù)
Mà ∠(CAE) =90o⇒∠(HAC) +∠(EAN) =90o (4)
Trong tam giác vuông AHC, ta có:
∠(AHC) =90o⇒∠(HAC) +∠(HCA) =90o (5)
Từ (4) và (5) suy ra: ∠(HCA) =∠(EAN) ̂
Xét hai tam giác vuông AHC và ENA, ta có:
∠(AHC) =∠(ENA) =90o
AC = AE (gt)
∠(HCA) =∠(EAN) ( chứng minh trên)
Suy ra : ΔAHC= ΔENA(cạnh huyền, góc nhọn)
Vậy AH = EN (hai cạnh tương ứng)
Từ (3) và (6) suy ra: DM = EN
Vì DM ⊥ AH và EN ⊥ AH (giả thiết) nên DM // EN (hai đường thẳng cùng vuông góc với đường thẳng thứ ba)
Gọi O là giao điểm của MN và DE
Xét hai tam giác vuông DMO và ENO, ta có:
∠(DMO) =∠(ENO) =90o
DM= EN (chứng minh trên)
∠(MDO) =∠(NEO)(so le trong)
Suy ra : ΔDMO= ΔENO(g.c.g)
Do đó: DO = OE ( hai cạnh tương ứng).
Vậy MN đi qua trung điểm của DE
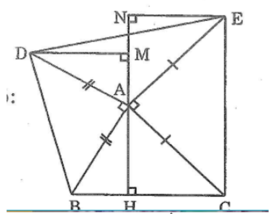

1) Vẽ hình..
2) Bài Làm
a, Ta có: BAHˆ+DAMˆ=90oBAH^+DAM^=90o;BAHˆ+ABHˆ=90oBAH^+ABH^=90o
⇒⇒DAMˆ=ABHˆDAM^=ABH^
Xét tam giác ADM vuông tại M và tam giác BAH vuông tại H ta có:
AD=BA(gt);DAMˆ=ABHˆDAM^=ABH^ (cmt)
Do đó tam giác ADM=tam giác BAH(cạnh huyền - góc nhọn)
=> DM=AH(cặp cạnh tương ứng) (đpcm)
b, Ta có: HACˆ+NAEˆ=90oHAC^+NAE^=90o;HACˆ+ACHˆ=90oHAC^+ACH^=90o
⇒⇒ NAEˆ=ACHˆNAE^=ACH^
Xét tam giác AEN vuông tại N và tam giác CAH vuông tại H ta có:
AE=CA(gt); NAEˆ=ACHˆNAE^=ACH^ (cmt)
Do đó tam giác AEN=tam giác CAH(cạnh huyền - góc nhọn)
=> EN=AH(cặp cạnh tương ứng)
mà DM=AH(cm câu a)
nên EN=DM
Gọi giao điểm của MN và DE là I (bạn tự thêm điểm trên hình nha mình quên)
Ta có: 90o−DIMˆ=90o−EINˆ→IDMˆ=IENˆ90o−DIM^=90o−EIN^→IDM^=IEN^
Xét tam giác DMI và tam giác ENI ta có:
DMIˆ=ENIˆ(=90o)DMI^=ENI^(=90o);DM=EN(đã cm);MDIˆ=NEIˆMDI^=NEI^(cmt)
Do đó tam giác DMI=tam giác ENI(g.c.g)
=> DI=EI(cặp cạnh tương ứng)
=> MN đi qua trung điểm của DE(đpcm)
Xét tam giác AND và BHA có:
DA = AB ( gt )
DNA = AHB ( = 90độ )
NDA=BAH(cùng phụ với DAN)
=>tam giác AND=BHA(ch-gn)
=>DN=AH nối A với E.giao diem giữa MNvà DE là O
vì DM VUÔNG GÓC AH EN VUÔNG GÓC AH =>DM song song
EN =>góc MEO=MDO XÉT TAM GIÁC MEA VÀ HAC CÓ
EA=AC
AME=AHC
MAE=ACH
=>TAM GIÁC MEA=HAC
=>ME=AH MÀ DM=AH
=>ME=DM
XÉT TAM GIÁC DNO VÀ EMO CÓ
DN=ME
DMN=ENM
EDM=NEO
=>TAM GIÁC DNO=NEO=>DO=OE
MN đi qua trung điểm DE