KU
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 10 2021
\(\overrightarrow{BM}+\overrightarrow{CN}+\overrightarrow{AP}\)
\(=\dfrac{1}{2}\left(\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{AP}\right)\)
\(=\overrightarrow{0}\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
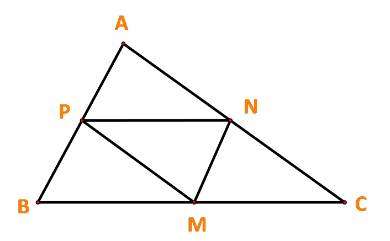
a) Ta có: \(\overrightarrow {BC} ,\overrightarrow {PN} \) là hai vecto cùng hướng và \(\frac{1}{2}\left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {PN} } \right|\)
\( \Rightarrow \frac{1}{2}\overrightarrow {BC} = \overrightarrow {PN} \)\( \Rightarrow \overrightarrow {AP} + \frac{1}{2}\overrightarrow {BC} = \overrightarrow {AP} + \overrightarrow {PN} = \overrightarrow {AN} \)
b) Ta có: \(\overrightarrow {MP} ,\overrightarrow {CA} \) là hai vecto cùng hướng và \(2\left| {\overrightarrow {MP} } \right| = \left| {\overrightarrow {CA} } \right|\)
\( \Rightarrow 2\overrightarrow {MP} = \overrightarrow {CA} \)\( \Rightarrow \overrightarrow {BC} + 2\overrightarrow {MP} = \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow {BA} \)
nên 
2 tháng 8 2023
a: Xét (O) có
góc BEC, góc BDC đều là các góc nội tiếp chắn nửa đường tròn
=>góc BEC=góc BDC=90 độ
=>CE vuông góc AB, BD vuông góc AC
Xét ΔABC có
CE,BD là đường cao
CE cắt BD tại H
=>H là trực tâm
=>AH vuông góc BC tại F
góc BEH+góc BFH=180 độ
=>BEHF nội tiếp
b: Xét ΔHCB có CO/CB=CM/CH
nên OM//BH
=>góc COM=góc CBH
=>góc COM=góc FEC
=>góc MOF+góc FEM=180 độ
=>OMEF nội tiếp
MH
17 tháng 12 2023
a) Ta có:
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)
\(=\overrightarrow{AB}+k\overrightarrow{BC}\)
\(=\overrightarrow{AB}+k\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
\(=\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\)
b) \(\overrightarrow{NP}=\overrightarrow{AP}-\overrightarrow{AN}\)
\(=\dfrac{2}{3}\overrightarrow{AC}-\dfrac{3}{4}\overrightarrow{AB}\)
Để \(AM\perp NP\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{NP}=\overrightarrow{0}\)
\(\Rightarrow\left[\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\right]\left(-\dfrac{3}{4}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\dfrac{3\left(k-1\right)}{4}AB^2+\dfrac{2k}{3}AC^2+\dfrac{2\left(1-k\right)}{3}\overrightarrow{AB}.\overrightarrow{AC}-\dfrac{3k}{4}\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{0}\)
\(\Leftrightarrow\dfrac{3\left(k-1\right)}{4}AB^2+\dfrac{2k}{3}AB^2+\dfrac{1-k}{3}AB^2-\dfrac{3k}{8}AB^2=0\)
\(\Leftrightarrow AB^2\left[\dfrac{3\left(k-1\right)}{4}+\dfrac{2k}{3}+\dfrac{1-k}{3}-\dfrac{3k}{8}\right]=0\)
\(\Leftrightarrow18\left(k-1\right)+16k+8\left(1-k\right)-9k=0\left(AB>0\right)\)
\(\Leftrightarrow17k=10\)
\(\Leftrightarrow k=\dfrac{10}{17}\)
20 tháng 12 2021
\(VT=\overrightarrow{AM}+\overrightarrow{BN}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{BC}\right)=\dfrac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{BC}\right)=-\dfrac{1}{2}\left(\overrightarrow{CA}+\overrightarrow{CB}\right)=\overrightarrow{PC}=VP\)
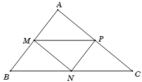
NP là đường trung bình của tg ABC \(\Rightarrow NP=\frac{AB}{2}=AM\)
\(\Rightarrow MP+NP=MP+AM\)
Xét tg AMP có
\(MP+AM>AP\) (Trong tg tổng 2 cạnh lớn hơn cạnh còn lại)
=> Bạn xem lại đề bài