Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thay ![]() = x ;
= x ; ![]() là y nhé bạn =='.
là y nhé bạn =='.
Theo đề bài ta có :
\(\left\{{}\begin{matrix}x+y=23\\x\cdot y=132\\y-x=1\end{matrix}\right.\left(ĐK:x,y>0\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=23-y\\x\cdot y=132\\y-\left(23-y\right)=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=23-y\\x\cdot y=132\\2y=24\Rightarrow y=12\end{matrix}\right.\)
Thay y = 12 vào hai đẳng thức trên ta được :
\(x+12=23\Rightarrow x=11\) hay \(x\cdot12=132\Rightarrow x=11\)
Vậy \(\left\{{}\begin{matrix}x=11\\y=12\end{matrix}\right.\) hay ![]() \(=11\);
\(=11\); ![]() \(=12\).
\(=12\).

a) 2323 . 474747 - 4747 . 232323
= 23 . 101 . 47 . 10101 - 101 . 47 . 23 . 10101
= 0 (Vì số bị trừ = số trừ)

\(VT=\dfrac{1+cos2x}{cos2x}\times\dfrac{1+cos4x}{sin4x}\) (*)
Ta có: theo công thức hạ bậc có: \(cos^2x=\dfrac{1+cos2x}{2}\Leftrightarrow1+cos2x=2cos^2x\) (1)
Ta có: \(cos2x=1-sin^2x\Rightarrow cos4x=1-2sin^22x\) (2)
Tương Tự có \(sin2x=2sinx\times cosx\Rightarrow sin4x=2sin2x\times cos2x\) (3)
Thay (1),(2),(3) vào (*) ta được: \(VT=\dfrac{2cos^2x}{cos2x}\times\dfrac{1+\left(1-2sin^22x\right)}{2sin2x\times cos2x}\)
\(VT=\dfrac{2cos^2x\times2\left(1-sin^22x\right)}{cos^22x\times2sin2x}\) mà \(1-sin^22x=cos^22x\)
\(\Rightarrow VT=\dfrac{2cos^2x\times cos^22x}{cos^22x\times2sinx\times cosx}=\dfrac{cosx}{sinx}=tanx\left(đpcm\right)\)
đoạn cuối nhầm nha \(VT=\dfrac{cosx}{sinx}=cotx\left(đpcm\right)\)

\(S=12+14+16+.......+1024\)
Từ 12 đến 1024 có số lượng số hạng là:
\(\left(1024-12\right):2+1=507\)
Ta có:
\(S=12+14+16+........+1024\)
\(=\dfrac{\left(12+1024\right).507}{2}=262626\)
\(M=21+24+27+........+369\)
Từ 21 đến 369 có số lượng số hạng là:
\(\left(369-21\right):3+1=117\)
Ta có:
\(M=21+24+27+........+369\)
\(=\dfrac{\left(21+369\right).117}{2}=22815\)
Chúc bạn học tốt!!!


Mk ghi lộn đề rùi![]()
bài 110 sgk trang 49 toán lop 6. Xl nhá![]()




Chọn B.
Do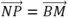 nên
nên