Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

https://olm.vn/hoi-dap/detail/204652944487.html tham khao nha
A,Xét \(\Delta AME\)và\(\Delta DMB\)có
AM=DM (gt)
BM=EM (gt)
AME^=DMB^ (đối đỉnh)
\(=>\Delta AME=\Delta DMB\left(c-g-c\right)\)
\(=>AE=BD\)
B,Xét \(\Delta AMF\)và \(\Delta DMC\)có:
\(DM=AM\left(gt\right)\)
\(CM=FM\left(gt\right)\)
AMF^=CMC^(Đối đỉnh)
\(=>\Delta AMF=\Delta DMC\left(c-g-c\right)\)
=>FAM^=CDM^
Do 2 góc này = nhau và ở vị trí sole
\(=>AF//DC\)
C,theo câu A ta có : EAM^=BDM^
=>AE//BD
theo câu B ta có :
AF//DC

Bạn tự vẽ hình nhé !
a, Xét tam giác AEM và tam giác DBM , ta có:
Góc BMD= góc AME ( 2 góc đối đỉnh)
DM=MA(gt)
ME=MB(gt)
do đó tam giác AEm= tam giác DBM(c-g-c)
suy ra : AE=BD( 2 cạnh tưởng ứng)
b, Xét tam giác MDC= tam giác MAF , ta có
Góc AMF= góc DMC ( đối đỉnh)
MF=MC (gt)
MA=MD(gt)
do đó tam gaisc MDC= tam giác MAF (c-g-c)
suy ra : góc FAM = góc CMD (2 góc tưởng ứng) và ở vị trí 2 góc so le trong nên AF // BC
c, Ta có :góc MAE= góc MDB (tam giác ADE= tam giác DMB) và ở vị trí so le trong nên AE // BC
mà AF// BC (câu b)
Theo tiên đề Ơ-clit thì 2 đường thẳng AE và AF trùng nhau nên 3 điểm A,E,F thẳng hàng .
Chúc bạn học tốt !!!

a) Vì AM là phân giác của góc BAC
nên góc BAM = CAM
Xét ΔBAM và ΔCAM có:
AB = AC ( giả thiết )
Góc BAM = CAM ( chứng minh trên )
AM cạnh chung.
=> Δ BAM = ΔCAM ( c.g.c )
=> BM = CM ( 2 cạnh tương ứng )
mà M nằm giữa B và C
Do đó M là trung điểm của BC → ĐPCM.
b) Ta có: AB + BE = AE
AC + CF = AF
mà AB = AC ( đề bài ); AE = AF (đề bài)
=> BE = CF.
Do ΔBAM = ΔCAM nên góc ABC = ACB ( 2 góc tương ứng )
Lại có: Góc ABC + CBE = 180 độ (kề bù)
Góc ACB + BCF = 180 độ (kề bù)
=> ABC + CBE = ACB + BCF
=> Góc CBE = BCF.
Xét ΔBCE và ΔCBF có:
BE = CF ( chứng minh trên)
Góc CBE = BCF ( chứng minh trên)
BC cạnh chung ( theo hình vẽ)
=> ΔBCE = ΔCBF ( c.g.c ) → ĐPCM.
c) Lại do ΔBCE = ΔCBF nên góc EBC = FCB ( 2 góc tương ứng ) hay góc EBM = FCM
Xét ΔMBE và ΔMCF có:
MB = MC ( chứng minh ở câu a )
Góc EBM = FCM ( chứng minh trên)
BE = FC ( chứng minh ở câu b)
=> ΔMBE = ΔMCF ( c.g.c )
=> ME = MF ( 2 cạnh tương ứng ) → ĐPCM.
d) Xét ΔEMN và ΔFMN có:
EM = FM ( chứng minh ở câu c )
EN = FN ( N là trung điểm EF )
MN chung.
=> ΔEMN = ΔFMN.
=> Góc ENM = FNM (2 góc tương ứng)
Suy ra MN là tia phân giác của góc ENF (1)
Có: góc BAM = CAM
Suy ra AM là tia phân giác của góc BAC (2)
Từ (1) và (2) suy ra A, M, N nằm trên cùng 1 đường thẳng.
Do đó A, M, N thẳng hàng → ĐPCM.

Xem nào, để chứng minh được thì phải vẽ hình ra đã, sau đó dựa theo công thức là làm được thôi anh/chị ạ. Em học lớp 6 nhưng học qua cái này rồi nên cũng biết sơ sơ một chút thui....

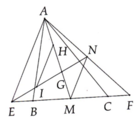




a: Xét ΔAHE và ΔCHB có
HA=HC
\(\widehat{AHE}=\widehat{CHB}\)
HE=HB
Do đó: ΔAHE=ΔCHB
b: Xét tứ giác ABCE có
H là trung điểm của BE
H là trung điểm của AC
Do đó:ABCE là hình bình hành
Suy ra: AE//BC và AE=BC
=>AF//BC và AF=BC
c: Xét tứ giác AFBC có
AF//BC
AF=BC
Do đó: AFBC là hình bình hành
=>AB cắt FC tại trung điểm của mỗi đường
=>F,N,C thẳng hàng