Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

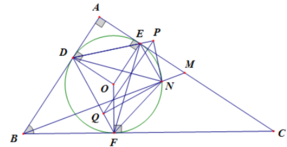
Vì DPN+DQN=90o+90o=180o nên DPNQ là tứ giác nội tiếp
=>QPN=QDN (hai góc nội tiếp cùng chắn cung QN) (5)
Mặt khác DENF là tứ giác nội tiếp nên QDN=FEN (6)
Từ (5) và (6) ta có FEN=QPN (7)
Tương tự ta có: EFN=PQN (8)
Từ (7) và (8) suy ra Δ N P Q ~ Δ N E F ( g . g ) = > P Q E F = N Q N F
Theo quan hệ đường vuông góc – đường xiên, ta có
N Q ≤ N F = > P Q E F = N Q N F ≤ 1 = > P Q ≤ E F
Dấu bằng xảy ra khi Q ≡ F ⇔ NF ⊥ DF ⇔ D, O, N thẳng hàng.
Do đó PQ max khi M là giao điểm của AC và BN, với N là điểm đối xứng với D qua O.

a) Nối DA. Ta thấy ngay \(\Delta BDI=\Delta BFI\left(c-g-c\right)\Rightarrow\widehat{BDI}=\widehat{BFI}\Rightarrow\widehat{ODI}=\widehat{OFI}\)
Lại có \(\widehat{OFI}=\widehat{OEF}\) (Do OE = OF)
Vậy nên \(\widehat{ODI}=\widehat{OEI}\) hay tứ giác DOIE nội tiếp. Vậy \(\widehat{DIO}=\widehat{DEO}=45^o\) (CM được ADOE là hình vuông)
Do \(\Delta BDI=\Delta BFI\left(c-g-c\right)\Rightarrow\widehat{BID}=\widehat{BIF}\)
Vậy \(\widehat{BIF}=45^o\)
b) Nếu AB = AM thì DE // BM . Khi đó \(\widehat{EHM}=\widehat{DEH}=\widehat{DEO}+\widehat{OEF}=45^o+\widehat{OEF}=\widehat{BIF}+\widehat{OFE}=\widehat{BOF}\)
Lại có \(\widehat{BHF}=\widehat{EHM}\Rightarrow\widehat{BHF}=\widehat{BOF}\) hay BOHF là tứ giác nội tiếp. Vậy \(\widehat{BHO}=90^o\)
Do AB = AM nên OB = OM . Vậy OH là đường cao đồng thời trung tuyến. Vậy H là trung điểm BM.
Suy ra AH là phân giác góc A hay \(\widehat{BAH}=45^o=\widehat{BIH}\Rightarrow\) ABHI là tứ giác nội tiếp.
c) PQ là dây cùng của đường tròn đường kính DM nên PQ lớn nhất khi DM lớn nhất. Vậy gọi N là điểm đối xứng với D qua O. Khi M là giao điểm của BN với AO thì PQ lớn nhất. Khi đó PQ = EF.
Đường tròn c: Đường tròn qua D với tâm O Đoạn thẳng f: Đoạn thẳng [A, C] Đoạn thẳng h_1: Đoạn thẳng [B, C] Đoạn thẳng n: Đoạn thẳng [B, A] Đoạn thẳng p: Đoạn thẳng [E, F] Đoạn thẳng r: Đoạn thẳng [B, I] Đoạn thẳng s: Đoạn thẳng [O, E] Đoạn thẳng t: Đoạn thẳng [D, O] Đoạn thẳng a: Đoạn thẳng [F, O] Đoạn thẳng b: Đoạn thẳng [D, I] Đoạn thẳng d: Đoạn thẳng [B, M] Đoạn thẳng e: Đoạn thẳng [D, E] Đoạn thẳng k_1: Đoạn thẳng [D, F] Đoạn thẳng l_1: Đoạn thẳng [E, P] Đoạn thẳng m_1: Đoạn thẳng [N, P] Đoạn thẳng n_1: Đoạn thẳng [Q, N] Đoạn thẳng p_1: Đoạn thẳng [Q, P] A = (-1.98, -4.46) A = (-1.98, -4.46) A = (-1.98, -4.46) C = (7.28, -4.44) C = (7.28, -4.44) C = (7.28, -4.44) Điểm B: Điểm trên g Điểm B: Điểm trên g Điểm B: Điểm trên g Điểm O: Giao điểm đường của j, k Điểm O: Giao điểm đường của j, k Điểm O: Giao điểm đường của j, k Điểm D: Giao điểm đường của g, m Điểm D: Giao điểm đường của g, m Điểm D: Giao điểm đường của g, m Điểm E: Giao điểm đường của c, f Điểm E: Giao điểm đường của c, f Điểm E: Giao điểm đường của c, f Điểm F: Giao điểm đường của c, h_1 Điểm F: Giao điểm đường của c, h_1 Điểm F: Giao điểm đường của c, h_1 Điểm I: Giao điểm đường của q, p Điểm I: Giao điểm đường của q, p Điểm I: Giao điểm đường của q, p Điểm M: Điểm trên f Điểm M: Điểm trên f Điểm M: Điểm trên f Điểm H: Giao điểm đường của p, d Điểm H: Giao điểm đường của p, d Điểm H: Giao điểm đường của p, d Điểm N: Giao điểm đường của c, d Điểm N: Giao điểm đường của c, d Điểm N: Giao điểm đường của c, d Điểm Q: Giao điểm đường của f_1, i_1 Điểm Q: Giao điểm đường của f_1, i_1 Điểm Q: Giao điểm đường của f_1, i_1 Điểm P: Giao điểm đường của g_1, j_1 Điểm P: Giao điểm đường của g_1, j_1 Điểm P: Giao điểm đường của g_1, j_1


1. Vì BD, BF là các tiếp tuyến của (O) nên OD ⊥ BD, OF ⊥ BF.
Xét 2 tam giác vuông OBD và OBF có
O B chung OBD=OBF(gt) = > Δ O B D = Δ O B F (cạnh huyền–góc nhọn)
⇒ BD = BF
Mà OD = OF = r nên OB là trung trực của DF ⇒ OB ⊥ DF ⇒ ∆ KIF vuông tại K.
Mà OD = OF = r nên OB là trung trực của DF ⇒ OB ⊥ DF ⇒ ∆ KIF vuông tại K. D O E = 90 o
Theo quan hệ giữa góc nội tiếp và góc ở tâm cho đường tròn (O), ta có:
D F E = 1 2 D O E = 45 o
⇒ ∆ KIF vuông cân tại K.
=>BIF=45o