Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
giúp mình câu này nhé,ghi rõ ra cho mình luôn và cả hình nữa,cảm ơn mọi người

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật

a: Xét tứ giác AEDF có
góc AED=góc AFD=góc FAE=90 độ
nên AEDF là hình chữ nhật
b: Xét ΔABC có CF/CA=CD/CB
nên DF//AB và DF=AB/2
=>Di//AB và DI=AB
=>ABDI là hình bình hành

a)Ta có
BK=KC (GT)
AK=KD( Đối xứng)
suy ra tứ giác ABDC là hình bình hành (1)
mà góc A = 90 độ (2)
từ 1 và 2 suy ra tứ giác ABDC là hình chữ nhật
b) ta có
BI=IA
EI=IK
suy ra tứ giác AKBE là hình bình hành (1)
ta lại có
BC=AD ( tứ giác ABDC là hình chữ nhật)
mà BK=KC
AK=KD
suy ra BK=AK (2)
Từ 1 và 2 suy ra tứ giác AKBE là hình thoi
c) ta có
BI=IA
BK=KC
suy ra IK là đường trung bình
suy ra IK//AC
IK=1/2AC
mà IK=1/2EK
Suy ra EK//AC
EK=AC
Suy ra tứ giác AKBE là hình bình hành
B A C D E K

a: Xét tứ giác AEDF có
AE//DF
DE//AF
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật
a, Vì DE//AB nên DE⊥AC và DF//AC nên DF⊥AB
Vì \(\widehat{AED}=\widehat{AFD}=\widehat{EAF}=90^0\) nên AEDF là hcn
b,Vì E là trung điểm MD và AC nên AMCD là hbh
Mà AC⊥DE nên AMCD là hthoi
c, Vì D là trung điểm BC và AK và \(\widehat{BAC}=90^0\) nên ABKC là hcn
Để ABKC là hv thì AB=AC hay tam giác ABC vuông cân tại A
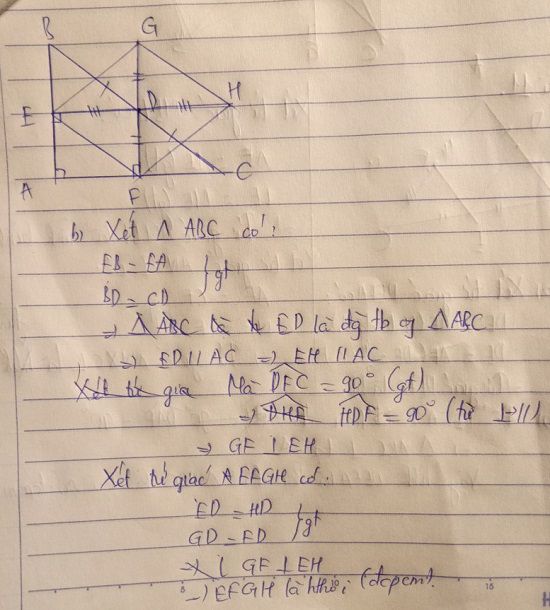

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
b: Xét ΔABC có
D là trung điểm của BC
DE//AC
Do đó: E là trung điểm của AB
Xét tứ giác AIBD có
E là trung điểm của AB
E là trung điểm của ID
Do đó: AIBD là hình bình hành
mà AB\(\perp\)DI
nên AIBD là hình thoi