Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đố các bạn
bé kia chăn vịt khác thường
buộc đi cho được chẵn hàng mới ưa
hàng 2 xếp thấy chưa vừa,
hàng 3 xếp vẫn còn thừa 1 con,
hàng 4 xếp vẫn chưa tròn,
hàng 5 xếp thiếu 1 con mới đầy
xếp thành hàng 7, đẹp thay!
vịt bao nhiêu ? tính được ngay mới tài !

a, xét tam giác ABD và tam giác EBD có: BD chung
góc ABD = góc EBD do BD là pg của góc ABC (gt)
AB = BE (gt)
=> tam giác ABD = tam giác EBD (c-g-c)
b, tam giác ABD = tam giác EBD (câu a)
=> góc DAB = góc DEB (đn)
mà góc DAB = 90
=> góc DEB = 90
tam giác ABD = tam giác EBD => DA = DE
xét tam giác MDA và tam giác CDE có : góc DAM = góc DEC = 90
goc MDA = góc CDE (đối đỉnh)
=> tam giác MDA = tam giác CDE (cgv-gnk)

Cho tam giác ABC vuông tại A. tia phân giác của góc ABC cắt AC tại D. lấy E trên cạnh BC sao cho BE = AB.
a) Chứng minh :tan giác ABD = tam giác EBD.
b) Tia ED cắt BA tại M. chứng minh : EC = AM
c) Nối AE. Chứng minh : góc AEC = góc EAM
b,VÌ \(\Delta ABD=\Delta EBD\)nên
AD=DE ( hai cạnh tương ứng)
Xét \(\Delta MAD\)và \(\Delta DEC\)có:
\(\widehat{MAD}=\widehat{DEC}=90^o\)
AD=DE (cmt)
\(\widehat{ADM}=\widehat{ADC}\)( 2 gíc đối đỉnh)
=> AM=EC( hai cạn tương ứng ) (đpcm)

a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó:ΔABD=ΔEBD
b: Xét ΔADM vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADM}=\widehat{EDC}\)
Do đó:ΔADM=ΔEDC
Suy ra: \(\widehat{BME}=\widehat{BCA}\)
Xét ΔBEM vuông tại E và ΔBAC vuông tại A có
BE=BA
\(\widehat{EBM}\) chung
Do đó:ΔBEM=ΔBAC
Suy ra: ME=CA

Lời giải:
a. Xét tam giác $ABD$ và $EBD$ có:
$AB=EB$
$BD$ chung
$\widehat{ABD}=\widehat{EBD}$ (do $BD$ là phân giác $\widehat{B}$)
$\Rightarrow \triangle ABD=\triangle EBD$ (c.g.c)
b.
Từ tam giác bằng nhau phần a suy ra:
$AD=DE$
$\widehat{BED}=\widehat{BAD}=90^0$
$\Rightarrow DE\perp BC$
$\Rightarrow \widehat{DEC}=90^0$
Xét tam giác $ADM$ và $EDC$ có:
$AD=ED$ (cmt)
$\widehat{ADM}=\widehat{EDC}$ (đối đỉnh)
$\widehat{DAM}=\widehat{DEC}=90^0$
$\Rightarrow \triangle ADM=\triangle EDC$ (g.c.g)
$\Rightarrow AM=EC$
c.
Từ tam giác bằng nhau phần b suy ra:
$\widehat{M_1}=\widehat{C_1}$
$DM=DC$
Mà $DE=AD$
$\Rightarrow DM+DE=DC+AD$
$\Rightarrow ME=AC$
Xét tam giác $AEM$ và $EAC$ có:
$AM=EC$ (cmt)
$EM=AC$ (cmt)
$\widehat{M_1}=\widehat{C_1}$ (cmt)
$\Rightarrow \triangle AEM=\triangle EAC$ (c.g.c)
$\Rightarrow \widehat{EAM}=\widehat{AEC}$

a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD

A)Xét tam giác ABD và EBD
DB chung
\(\widehat{EBD}=\widehat{DBA}\)
AB=AE
=> tam giác ABD = tam giác EBD
B)DE=AD
DE\(⊥\)BC
Xét tam giác vuông DEC và DAM
\(\widehat{CDE}=\widehat{MDA}\)
AD=DE
=> tam giác ADM = tam giác EDC => CE =AM
C) MÌNH KO BIẾT

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: Xét ΔBDF và ΔEDC có
\(\widehat{BDF}=\widehat{EDC}\)
DB=DE
\(\widehat{DBF}=\widehat{DEC}\)
Do đó: ΔBDF=ΔEDC
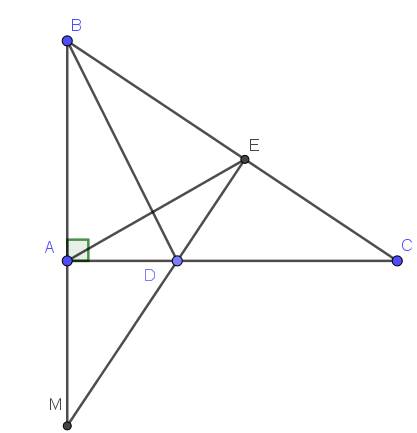
a) Xét: tam giác ABD và tam giác EBD có:
.AB= BE (giả thiết)
.góc B1= góc B2 (giả thiết)
.BD cạnh chung
suy ra: tam giác ABD= tam giác EBD (c-g-c)
b) Xét: tam giác ADM vuông tại A và tam giác CDE vuông tại E có:
.MD=ME ( giả thiết)
.góc D1= gócD2 (đối đỉnh)
suy ra: tam giác ADM= tam giác EBD ( cạnh huyền- góc nhọn)
Ta có : tam giác ADM= tam giác EBD (cmt)
suy ra:EC= AM (2 cạnh tương ứng)
c) Xét: tam giác AEC vuông tại A và tam giác EAM vuông tại E có:
.AE=EM (giả thiết)
. góc C= góc M (giả thiết)
suy ra : tam giác AEC= tam giác EAM (c-h-g-n)
Ta có: tam giác AEC= tam giác EAM (cmt)
suy ra: góc AEC = góc EAM( 2 góc tương ứng)