Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

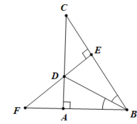
c. Xét ∆ADF và ∆EDC có:
AD = DE
∠(ADF) = ∠(EDC) (hai góc đối đỉnh)
⇒ ∆ADF = ∆EDC ( cạnh góc vuông – góc nhọn kề)(1 điểm)
⇒ DF = DC (hai cạnh tương ứng) (0.5 điểm)

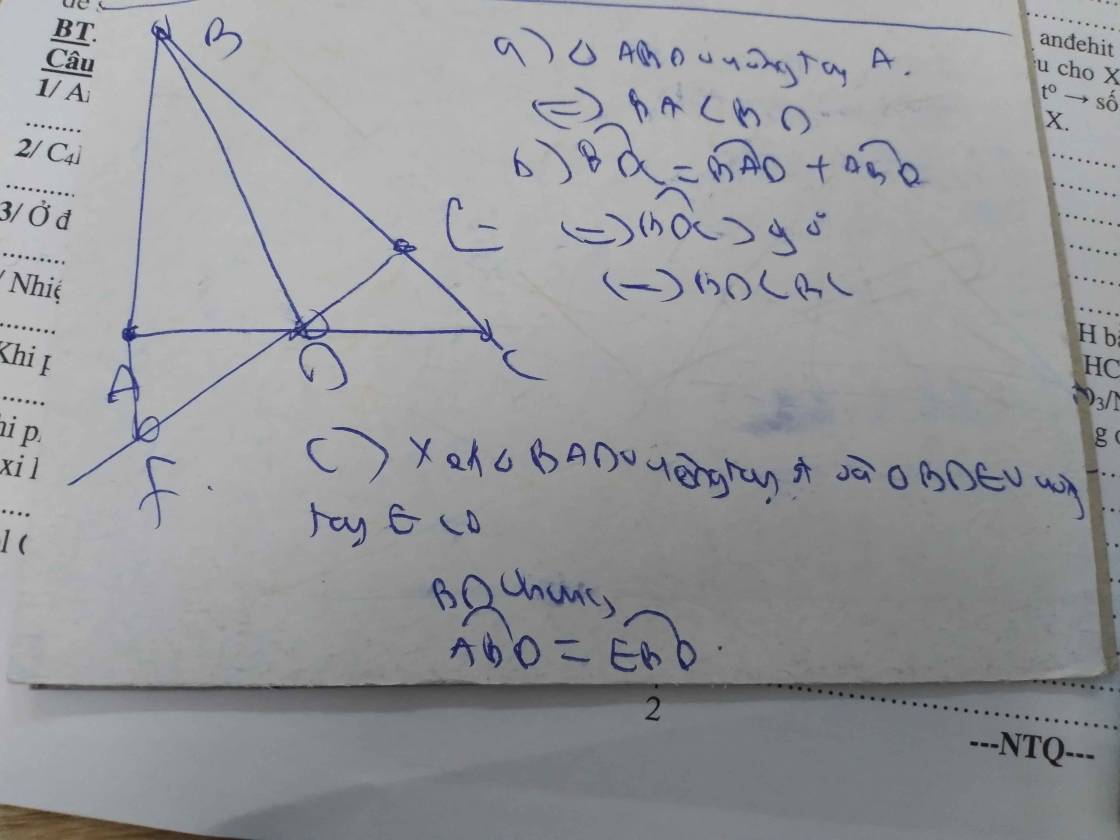
a. Hình vẽ (0.5 điểm)
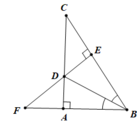
Xét ∆ABD và ∆EBD có:
∠(ABD) = ∠(DBE)
BD là cạnh chung
⇒ ∆ABD = ∆EBD(cạnh huyền – góc nhọn) (1 điểm)

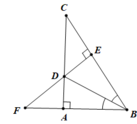
b. Ta có AB = BE ⇒ B nằm trên đường trung trực của AE (0.5 điểm)
Do ∆ABD = ∆EBD nên AD = DE (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AE
Vậy BD là đường trung trực của AE (0.5 điểm)

a) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(Cạnh huyền-góc nhọn)
Suy ra: AD=ED(Hai cạnh tương ứng)

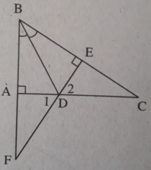
Xét ΔDEC vuông tại E:
DE < DC (cạnh góc vuông nhỏ hơn cạnh huyền)
Ta lại có DA = DE (câu a)) nên DA < DC.

a) Hai tam giác = nhau theo trường hợp cạnh huyền góc nhọn (tự c/m)
b) Từ 2 tam giác = nhau ở phần a => AD= DE
Ta có tam giác ADF = tam giác EDC theo trường hợp góc cạnh góc (tự c/m)
=> DF= DC ( 2 cạnh tg ứng)
c) Xét tam giác ADF, có : góc A= 90 độ
=> DF là cạnh lớn nhất (quan hệ giữa góc và cạnh đối diện)
=> AD < DF
Mà DF= DC (chứng minh b)
=> AD < DC (đpcm)
b) Xét tam giác ADF và tam giác EDC, có:
Góc A= góc E (=90 độ)
AD= AE (vừa mình đã ns rồi)
Góc ADF= góc EDC (đối đỉnh)
Từ 3 điều trên => tam giác ADF = tam giác EDC (g-c-g)
=> DF= DC (2 cạnh tg ứng)

a: Xét ΔABE vuông tại A và ΔDBE vuông tại D có
BE chung
\(\widehat{ABE}=\widehat{DBE}\)
Do đó: ΔABE=ΔDBE
b: Ta có: ΔABE=ΔDBE
=>BA=BD và EA=ED
Ta có: BA=BD
=>B nằm trên đường trung trực của AD(1)
Ta có: EA=ED
=>E nằm trên đường trung trực của AD(2)
Từ (1) và (2) suy ra BE là đường trung trực của AD
=>BE\(\perp\)AD
c: Xét ΔEAF vuông tại A và ΔEDC vuông tại D có
EA=ED
\(\widehat{AEF}=\widehat{DEC}\)(hai góc đối đỉnh)
Do đó: ΔEAF=ΔEDC
=>EF=EC
=>ΔEFC cân tại E

Sửa đề: F là giao điểm của tia BA và tia ED
Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
=>DA=DE
Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAF=ΔDEC
=>DF=DC
=>ΔDFC cân tại D

d. Trong tam giác vuông DEC có DC là cạnh huyên nên DC là cạnh lớn nhất
⇒ DC > DE mà DE = AD ⇒ DC > AD (1 điểm)