Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A M N H C B
Cho tam giác ABC có MN =15 cm NK =12 cm
Xét: Tam giác AHB (HBN) = 90 độ HM = đc
Xét tam giác AHC (AHC = 90 độ) có HN là đường cao
=> AH =An = AC (2)
Kết luận sơ sơ: Từ (1) (2) AM AB =AN=AC
...................... còn lại chịu -.-
~Study well~ :)

bạn tự vẽ hình nhé
b) Vì N là hình chiếu của M trên AC nên MN vuông góc với AC
=> MN//AB
Xét ΔABC có M là trung điểm của BC
MN//AB
=> N là trung điểm của AC
Xét ΔABC có M là trung điểm của BC
N là trung điểm của AC
=> MN là đường trung bình của ΔABC
=> MN = 1/2.AB
=> AB = 30 cm
Xét ΔMNC vuông tại N có NK là đường cao
=> \(\frac{1}{NK^2}=\frac{1}{MN^2}+\frac{1}{NC^2}\)
=> \(\frac{1}{144}=\frac{1}{225}+\frac{1}{NC^2}\)
=> NC = 20 cm
=> AC = 40 cm
=> diện tích ABC = AB.AC/2 = 30.40:2 = 600 cm2
Chúc bạn làm bài tốt

M là trug điểm BC
MN //AB
nên MN là đường trung bình của AB , AB=2MN=30
- Áp dụng hệ thức lương vào tam giác vuông MNC (vuông tại N)
ta có \(\frac{1}{NK^2}=\frac{1}{NM^2}+\frac{1}{NC^2}\)
=> ta tìm dc NC mà AC=2NC
vậy ta biết dc 2 cạnh AB và AC
diện h tam giác \(=\frac{1}{2}.AB.AC\)

muốn giúp lắm nhưng mới lớp 7 chỉ bt làm phần a,d nghĩ bài a,d là toán lớp 7

a.
\(AB^2+AC^2=4,5^2+6^2=56,25\)
\(BC^2=7,5^2=56,25\)
\(\Rightarrow AB^2+AC^2=BC^2\Rightarrow\Delta ABC\) vuông tại A theo Pitago đảo
b.
Theo định lý phân giác: \(\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow DB=\dfrac{3}{4}DC\)
Mà \(DB+DC=BC=7,5\)
\(\Rightarrow\dfrac{3}{4}DC+DC=7,5\Rightarrow DC=\dfrac{30}{7}\left(cm\right)\)
Do DN và AB cùng vuông góc AC \(\Rightarrow DN||AB\)
Áp dụng định lý Talet:
\(\dfrac{DN}{AB}=\dfrac{DC}{BC}=\dfrac{4}{7}\Rightarrow DN=\dfrac{4}{7}AB=\dfrac{18}{7}\left(cm\right)\)
Tứ giác AMDN là hình chữ nhật (có 3 góc vuông)
Mà AD là đường chéo đồng thời là phân giác theo giả thiết
\(\Rightarrow AMDN\) là hình vuông
\(\Rightarrow S_{AMDN}=DN^2=\dfrac{324}{49}\approx6,6\left(cm^2\right)\)
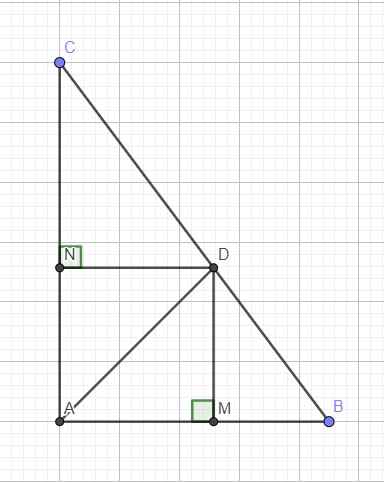
Gíup em vs ạ
A B C M N K
a) Áp dụng hệ thức lượng △NMC vuông tại N ta có :
\(\frac{1}{MN^2}+\frac{1}{NC^2}=\frac{1}{NK^2}\)
\(\Leftrightarrow\frac{1}{15^2}+\frac{1}{NC^2}=\frac{1}{12^2}\)
\(\Leftrightarrow NC=20\)cm
Ta có : △ABC vuông tại A có AM là đường trung tuyến (M thuộc BC)
=> AM = MC
=> △AMC cân tại M
=> MN đồng thời vừa là đường cao vừa là đường trung tuyến
=> AN = NC = \(\frac{AC}{2}\)
Mà NC = 20cm
=> AC = 40cm
=> \(S_{AMC}=\frac{40.15}{2}=300\left(cm^2\right)\)
Ta có : \(S_{AMC}=\frac{1}{2}S_{ABC}\)
vì có cùng độ dài đường cao và \(MC=\frac{1}{2}BC\)
Vậy \(S_{ABC}=600cm^2\)